Transportation Problem: Definition, Formulation, and Types
Transportation problems are used to find the minimum cost of transportation of goods from m source to n destination. In this article, we will learn about transportation problems, formulation, types and how they differ from assignment problems.
A transportation problem in operation research is a special type of Linear Programming Problem used to optimize (minimize) the transportation cost and allocate resources from M source to N destination. This article will briefly discuss transportation problems, types of transportation problems, and how to solve them.
So, let’s dive into learning all about Transportation Problems.
What is the Transportation Problem?
A transportation problem is a Linear Programming Problem that deals with identifying an optimal solution for transportation and allocating resources to various destinations and from one site to another while keeping the expenditure to a minimum.
In simple words, the main objective of the Transportation problem is to deliver (from the source to the destination) the resources at the minimum cost.
- It is also referred to as the Hitchcock Problem.
- It involves transporting a single product from ‘m’ source (origin) to ‘n’ destinations.
- Assumptions: The supply level of each source and the demand at each destination are known.
- Objective: To minimize the total Transportation Cost.
Acquire in-depth knowledge of Data Science. Enroll in our top programmes and online courses from the best colleges in India today to take the next step in your career!
Formulation of Transportation Problem
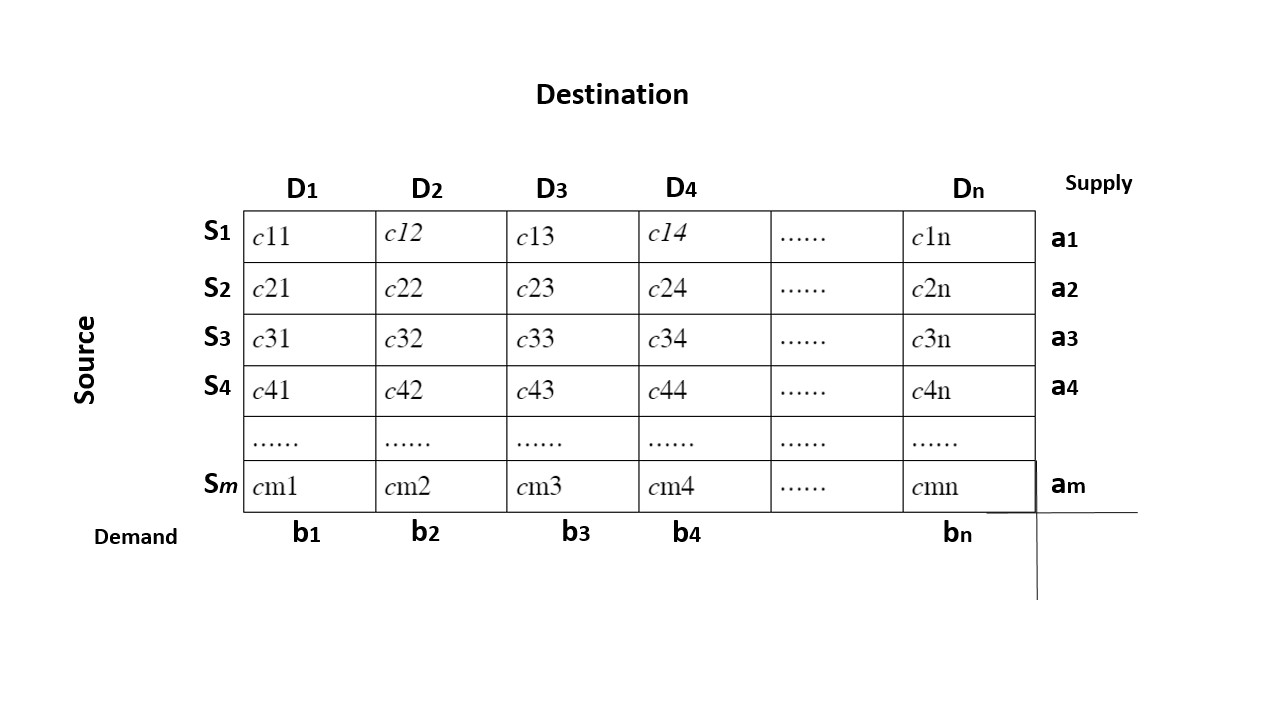
Let you are supplying the resources from m source (Si) to n destinations (Dj) such that:
ai: the quantity available at the source Si
bj: the quantity required at the destination Dj
cij: cost of transportation of one unit resource from Si to Dj
xij: units of resources transported from Si to Dj
1<= i <= m, 1 <= j <= n
So, the Total Cost of Transposition is:
(c11x11 + c12x12 + c13x13 + …… + c1nx1n) + (c21x21 + c22x22 + c23x23 + …… + c2nx2n) + …….. + (cm1xm1 + cm2xm2 + cm3xm3 + …… + cmnxmn)
As we already mentioned, our objective is to minimize the Total Cost:
Min Z = (c11x11 + c12x12 + c13x13 + …… + c1nx1n) + (c21x21 + c22x22 + c23x23 + …… + c2nx2n) + …….. + (cm1xm1 + cm2xm2 + cm3xm3 + …… + cmnxmn)
Subject to:
xi1 + xi2 + ……. + xin = ai & x1j + x2j + …….. + xmn = bj
xij >= 0,
i = 1, 2, 3, ……, m, j = 1, 2, 3, ……., n
The matrix below can also represent the above diagram.
Types of Transportation Problems
Transportation problems are broadly classified into balanced and unbalanced, depending on the source’s supply and the requirement at the destination.
Balanced Transportation Problem
Unbalanced Transportation Problem
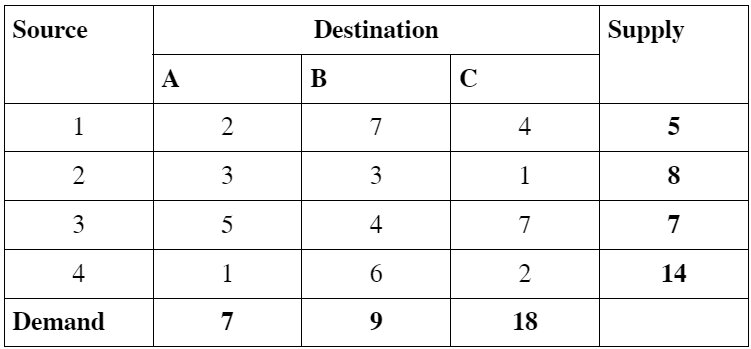
Example – 1: Check which types of Transportation Problem it is.
Answer – 1: From the above, we have
Total Supply = 5 + 8 + 7 + 14 = 34
Total Demand = 7 + 9 + 18 = 34
Hence, Total Supply = Total Demand
Therefore, it is a Balanced Transportation Problem.
Example – 2: Check whether the given problem is Balanced or Unbalanced.
| D1 | D2 | D3 | Availability | |
| S1 | 4 | 3 | 2 | 10 |
| S2 | 2 | 5 | 0 | 13 |
| S3 | 3 | 8 | 6 | 12 |
| Required | 8 | 5 | 4 | – |
Answer – 2: From the above matrix, we have:
Total Supply = 10 + 13 + 12 = 35
Total Demand = 8 + 5 + 4 = 17
Hence, Total Supply != Total Demand; therefore, the given transportation problem is an Unbalanced Transportation Problem.
Now, let’s see the difference between a transportation problem and an assignment problem.
Transportation Problem vs. Assignment Problem
| Transportation Problem | Assignment Problem |
| It is used to optimize the transportation cost. | It is about assigning a finite source to a finite destination (one source is alloted to one destination). |
| A number of Sources and demands may or may not be equal. | The number of sources and the number of destinations must be equal. |
| If demand and supply are not equal, then the transportation problem is known as the Unbalanced Transportation Problem. | If the number of rows and the number of columns are not equal, then the assignment problem is known as the Unbalanced Assignment Problem. |
| It requires two steps to solve:Find the Initial Solution using North West, Least Cost or Vogel ApproximationFind Optimal Solution using the MODI method. | It requires only one step to solve.The Hungarian Method is sufficient to find the optimal solutions. |
Must Check: Difference Between Transporation Problem and Assignment Problem
Conclusion
Transportation Problem in operational research is a special kind of linear programming problem, having an objective to find the minimum cost of transportation of goods from m source to n destination.
I hope this article helps you learn more about transportation problems in operational research.
Keep Learning!!
Keep Sharing!!
FAQs
What is Transportation Problem?
A transportation problem is a Linear Programming Problem that deals with identifying an optimal solution for transportation and allocating resources to various destinations and from one site to another while keeping the expenditure to a minimum.
What are the key elements of Transportation Problem?
The key elements of the Transporation problems are: 1. Source 2. Destination 3. Supply 4. Demand and 5. Transportation Cost
What is the objective of transportation problem?
The main of the transportation problem is to minimize the cost while meeting the demand requirements of each destination and supply cost requirements.
What are the different methods for solving transportation problem?
There are different methods to solve the transportations problem, such as: 1. NorthWest Corner Method, 2. Least Cost Method, 3. Vogel's Approximation Method, and 4. Steppingstone Method
What are the assumptions made in transportation problem?
The assumption for solving transportation problems are: 1. Transportation costs are linear and constant. 2. Supply and demand are fixed 3. Goods are homogeneous. 4. Sources and Destinations are mutually exclusive






Comments