Matrices
Get insights from 180 questions on Matrices, answered by students, alumni, and experts. You may also ask and answer any question you like about Matrices
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
We have, AB = BA. (given)
(E) P (n):AB' = B'A.
P (i):AB1 = B1A. Þ AB = BA
so, the result is true for n = 1.
Let the result be true for n = k.
P (k):ABk = BkA
Then,
P (k + 1) : ABk + 1 = A. Bk. B = BkA.B = Bk.BA
= Bk + 1.A .
So, ABk + 1 = Bk + 1A.
The result also holds for n = k + 1.
Hence, AB^n = B^n A^n holds for all natural number 'n'.
New answer posted
8 months agoContributor-Level 10
We have,
(E) (B'AB)' = [B' (AB]'
= (AB)' (B')'
= B'A'B.
When A is symmetric, A' = A
(B'AB)' = B'AB
ie, B'AB is symmetric.
And when A is skew-symmetric, A1 = -A
(B'AB)' = -B'AB.
ie, B'AB is skew-symmetric.
New answer posted
8 months agoContributor-Level 10
Given, A and B are symmetric matrices.
(E) Then A' = A and B' = B.
Now, (AB - BA)' = (AB)' - (BA)'
= B'A' - A'B'
= BA - AB
= - (AB - BA).
Hence, AB BA is skew-symmetric matrix
New answer posted
8 months agoContributor-Level 10
We have,
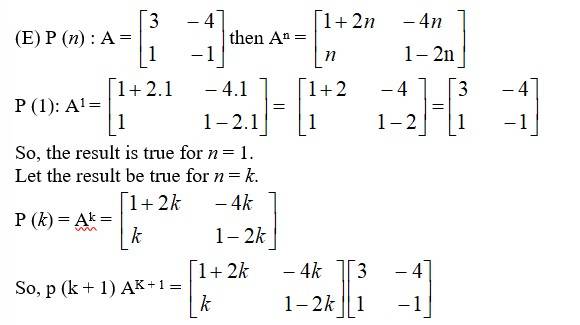
The results also holds for n = k + 1. Hence, An
Holds for all natural number n.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 686k Reviews
- 1800k Answers