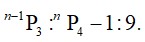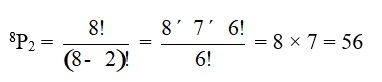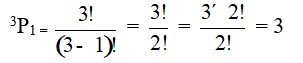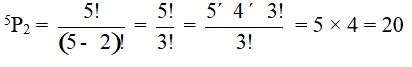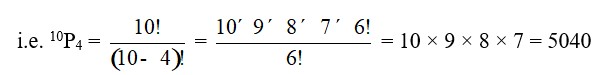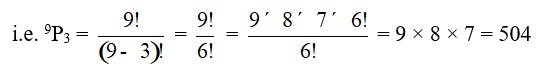Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
8 months agoContributor-Level 10
19. Since no letter is repeated in the word EQUATION.
The permutation of 8 letters taken all at a time
= 8P8
=
=
= 8! [since, 0! = 1]
= 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1
= 40320
New question posted
8 months agoNew answer posted
8 months agoContributor-Level 10
15. The permutation of 5 different digits namely 1, 2, 3, 4, 5 taken 4 at a time is
5P4 = = = 5 * 4 * 3 * 2 * 1 = 120
The permutation of having 2 or 4 at ones place is
2P1 = = = 1 * 2 = 2
After fixing one of the even number at last digit we can rearrange the remaining four digits taking 3 at a time. i.e.
4P3 = = = 4 * 3 * 2 * 1 = 24
Therefore, total permutation of 4 digit even number using 1, 2, 3, 4, 5
= 24 * 2
= 48
New answer posted
8 months agoContributor-Level 10
14. The permutation of having even number at the last digit from the given 6 different digits namely 1, 2, 3, 4, 5, 6 to form a 3-digit number is
After taking one of the even number as last digit we can rearrange the remaining 5 digits taking 2 at a time. i.e.
Therefore, The required number = 20 * 3 = 60
New answer posted
8 months agoContributor-Level 10
49. Here, out of 100 students, first section has 40 students and the rest I e, 60 students enters in second section.
As me and my friend are among the 100 students.
The no. of ways of selecting 2 students from the 100 students
= 100C2
(a) When both enters first section if 2 of us are among the 40 students that are to be selected. Similarly, if both enters second section among the 60 students for that section.
(if 2 of us)
Hence, no. of ways of selecting both in same section = 40C2 + 60C2
Probability that both of us are in same section

New answer posted
8 months agoContributor-Level 10
48. Total no. of ticket for lottery sold = 10, 000
No. of ticket that are awarded prize = 10
So, no. of ticket that are not awarded prize = 10.000 - 10
= 9990
(a) Now, probability of met getting a prize if we buy one ticket

New answer posted
8 months agoContributor-Level 10
13. For every four-digit number we have to count the permutation of 10 digits namely 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 taken 4 at a time
However, these permutation will include those where 0 is at 1000's place.
So, fixing 0 at 1000's place and rearranging the remaining 9 digits taking 3 at a time.
New answer posted
8 months agoContributor-Level 10
47. Since the die has two faces each mark 1, three faces each marks 2 and one face mark 3.
The possible sample space of outcome is.
S = {1, 2, 3} so, n (s) = 6
(i) P (2)
(ii) P (1 or 3) = P (1) + P (3) =
(iii) P (not 3) = 1 P (3) = 1 - =
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers