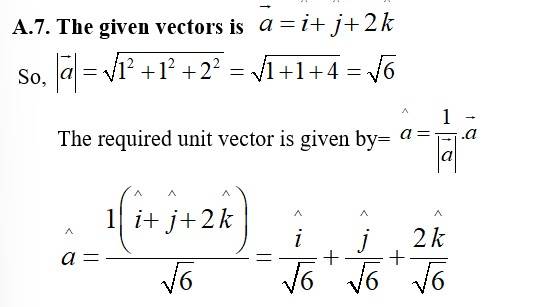Vector Algebra
Get insights from 117 questions on Vector Algebra, answered by students, alumni, and experts. You may also ask and answer any question you like about Vector Algebra
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Let,
It is seen that
Where,
Therefore, we can say that the given vector are collinear.
New answer posted
7 months agoContributor-Level 10
Let the vector with initial point P (2,1) and terminal point Q. (-5,7) can be shown as,
The scalar components are -7 and 6.
The vector components are -7i and 6j.
New answer posted
7 months agoContributor-Level 10
Note that two vector are equal only if their corresponding components are equal.
Thus, the given vectors and will be equal if and only if
New question posted
7 months agoTaking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers