Class 12th

$x={\displaystyle \sum _{n=0}^{\infty }co{s}^{2n}\theta =co{s}^0\theta +co{s}^2\theta +co{s}^4\theta +.....=1+co{s}^2\theta +co{s}^4\theta +.....}$  

a = 1, r = cos² θ

$x=S_{\infty }=\frac{a}{1-r}=\frac{1}{1-co{s}^2\theta }=\frac{1}{si{n}^2\theta }$           

Similarly, y = $\frac{1}{co{s}^2\theta }\Rightarrow \frac{1}{y}=co{s}^2\theta$  

$z=\frac{xy}{xy-1}\Rightarrow xyz-z=xy...........\left(i\right)$           

Also, $\frac{1}{x}+\frac{1}{y}=1\Rightarrow x+y=xy..........\left(ii\right)$  

 (i) & (ii) ->xyz = xy + z -> (x + y) z = xy + z

Let

A : Missile hit the target

B : Missile intercepted      

P (B) =    $\frac{1}{3}P\left(A/\overline{B}\right)=\frac{3}{4}$

$P\left(\overline{B}\right)=\frac{2}{3}$  

$\Rightarrow P\left(\overline{B}\cap A\right)=\frac{3}{4}*\frac{2}{3}=\frac{1}{2}$   

Required Probability = $\frac{2}{3}*\frac{3}{4}*\frac{2}{3}*\frac{3}{4}*\frac{2}{3}*\frac{3}{4}=\frac{1}{8}$  

$\underset{n\to \infty }{lim}{\left(1+\frac{1+\frac{1}{2}+.......+\frac{1}{n}}{n^2}\right)}^n$ limit is in the form of $1^{\infty }$  

$\mathcal{l}=exp\left(\underset{n\to \infty }{lim}\frac{1+\frac{1}{2}+\frac{1}{3}+.....+\frac{1}{n}}{n^2}\right)$             

$0\le 1+\frac{1}{2}+\frac{1}{3}+.....+\frac{1}{n}\le 1+\frac{1}{\sqrt[]{2}}+\frac{1}{\sqrt[]{3}}+....+\frac{1}{\sqrt[]{n}}\le 2\sqrt[]{n}-1$        

Taking limit   $\left(n\to \infty \right)$

$\mathcal{l}$ = exp (0) (from sandwich)

  $\mathcal{l}=1$          

Second Method :

$1+\frac{1}{2}+\frac{1}{3}+....+\frac{1}{n}\ge ln\left(n+1\right).......\left(i\right)$

$1+\frac{1}{2}+\frac{1}{3}+.....+\frac{1}{n}\le 1+{\displaystyle {\int }_1^2\frac{1}{2}dx\le 1+lnn..........\left(ii\right)}$

From (i) & (ii)

$ln\left(n+1\right)\le 1+\frac{1}{2}+\frac{1}{3}+....+\frac{1}{n}\le 1+Inn,\forall n\in N,n\ge 2$           

As $\underset{n\to \infty }{lim}\frac{ln\left(n+1\right)}{n}=0$  

and $\underset{n\to \infty }{lim}\frac{1+ln\left(n\right)}{n}=0$  

$\therefore$ from sandwich theorem

$\underset{n\to \infty }{lim}\frac{1+\frac{1}{2}+\frac{1}{3}+.....+\frac{1}{n}}{n}=0$  

$\therefore e^0=1$   

Yes, candidates can get admission in the BSc course at SIT Siliguri with 60% in Class 12. The institute has not specified the minimum required aggregate for the same, but, since 60% is a good score, candidates are eligible for admission. The institute accepts Class 12 merit for admissions in the BSc course. Candidates must fill out the application forms available online on the official website before the last date. 

$\overrightarrow{O}P=\left(2,-1,1\right)$

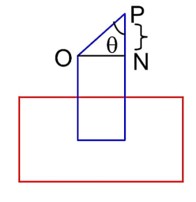
Normal vector to the plane

$=\overrightarrow{A}B*A\overrightarrow{C}=\left|\begin{array}{ccc}\hfill \widehat{i}\hfill & \hfill \widehat{j}\hfill & \hfill \widehat{k}\hfill \\ \hfill 1\hfill & \hfill 1\hfill & \hfill -2\hfill \\ \hfill 1\hfill & \hfill 2\hfill & \hfill -1\hfill \end{array}\right|=\left(3,-1,1\right)=\overrightarrow{n}$

Projection of $\overrightarrow{O}Pon\overrightarrow{n}is\left|\frac{\overrightarrow{O}P.\overrightarrow{n}}{\left|\overrightarrow{n}\right|}\right|$

PN = $\frac{6+1+1}{\sqrt[]{11}}=\frac{8}{\text{exception 25:}}$

$\frac{\text{exception 25:}}{}$Projection of OP on plane = ON =  $\sqrt[]{O{P}^2-P{N}^2}=\sqrt[]{6-\frac{64}{11}}=\sqrt[]{\frac{2}{11}}$

Yes, Global Institute of Management and Technology accept Class 12th marks for admission. Candidates seeking admission to the UG and Diploma programmes can enrol for admission with Class 12 marks. Candidates must complete Class 12 to enrol for various courses. The college offers more than 10 certificate courses. Global Institute of Management and Technology admissions are based on entrance-exam scores.

  $\frac{x^2}{a}+\frac{y^2}{b}=1,\frac{x^2}{c}-\frac{y^2}{\left(-d\right)}=1$

Ellipse and Hyperbola are orthogonal so these will be confocal.

$\sqrt[]{a-b}=\sqrt[]{c+\left(-d\right)}$            

a – b = c – d

$l={\displaystyle \int \frac{8x^3+20x^2}{x^4+5x^3-7x^2}}dx=4{\displaystyle \int \frac{2x+5}{x^2+5x-7}dx=4ln\left|x^2+5x-7\right|+c}$

$f\left(x\right)=x^3-a{x}^2+bx-4$

f (1) = f (2)

->1 – a + b – 4 = 8 – 4a + 2b – 4

->3a – b = 7 . (i)

8a = 16 + 3b . (ii)

(i) and (ii) -> (a, b) = (5, 8)

As per questions

$\frac{dy}{dx}=\frac{x^2-4x+y+8}{x-2}$           

$\frac{dy}{dx}=\frac{{\left(x-2\right)}^2+\left(y+4\right)}{\left(x-2\right)}$           

$\frac{dy}{dx}=\left(x-2\right)+\frac{y+4}{x-2}$                       .(i)

Let $\frac{y+4}{x-2}=t$  

(y + 4) = t(x – 2)

Putting in equation (i)

$\left(x-2\right)\frac{dt}{dx}+t=\left(x-2\right)+t$        

    $\frac{dt}{dx}=1$        

dt = dx

Integrating on both the sides t = x + c

$\frac{y+4}{x-2}=x+c$  

Passing through origin C = -2

  $\therefore$         equation of curve $\frac{y+4}{x-2}=x-2$