Logical Reasoning
Get insights from 271 questions on Logical Reasoning, answered by students, alumni, and experts. You may also ask and answer any question you like about Logical Reasoning
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
6 months agoContributor-Level 10
One of the men spent 2517 – 1378 = 1139, he is Aman. This is the only possibility as we add Rs. 1378 even to the least amount Rs. 1193, we will not be able to satisfy all the conditions given simultaneously.
So, the table obtained is:
Raman | Aman | Dev | Sanjay | Kamal |
2234 | 1139 | 1139 | 1340 | 2517 |
(c)
New answer posted
6 months agoContributor-Level 10
One of the men spent 2517 – 1378 = 1139, he is Aman. This is the only possibility as we add Rs. 1378 even to the least amount Rs. 1193, we will not be able to satisfy all the conditions given simultaneously.
So, the table obtained is:
Raman | Aman | Dev | Sanjay | Kamal |
2234 | 1139 | 1139 | 1340 | 2517 |
(a)
New answer posted
6 months agoContributor-Level 10
One of the men spent 2517 – 1378 = 1139, he is Aman. This is the only possibility as we add Rs. 1378 even to the least amount Rs. 1193, we will not be able to satisfy all the conditions given simultaneously.
So, the table obtained is:
Raman | Aman | Dev | Sanjay | Kamal |
2234 | 1139 | 1139 | 1340 | 2517 |
(b)
New answer posted
6 months agoContributor-Level 10
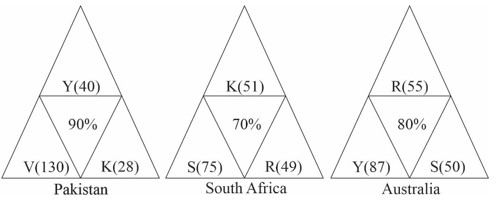
(b)
Y scored 127 in G1 and G3. V scored 130 in G1 itself.
K's mas score could be 28 + 51 + 48 = 127
R's mas score could be 49 + 55 + 22 = 126
S's mas score could be 75 + 50 + 22 = 147
Only R definitely scored less than Y.
Hence, option 2.
New answer posted
6 months agoContributor-Level 10
(c)
Form answer to the first question, the M-index of only R and S can be exactly calculated.
Hence, option (c)
New answer posted
6 months agoContributor-Level 10
(a)
If y2 < 40, then y's R-index = 87 y2 > 47; i.e. 47 < Y's R-index 87
If y2 > 40, then Y's R-index = 87 – 40 = 47
47 ≤ Y's R-index ≤ 87
Similarly,
23 ≤ K's R-index ≤ 51
33 ≤ S's R-index ≤ 55
53 ≤ S's R-index ≤ 75
82 ≤ V's R-index ≤ 130
Any one of Y, K or R could have the lowest R-index.
Hence, option (a).
New answer posted
6 months agoContributor-Level 10
(a)
Consider game against Pakistan (G1).
Runs scored by Y, V and K = 40 + 130 + 28 = 198
Total runs scored = 198/0.9 = 220
Runs scored by R (r1) and S (s1), r1, s1 < 28 and r1+ +s1? 22
Consider the game against South Africa (G2).
Runs scored by K, R and S = 51 + 49 + 75 = 175
Total runs scored = 175/0.7 = 250
Runs scored by Y (y2) and V (v2), y2, v2 < 49 and y2 + v2? 75
Consider the game against Australia (G3).
Runs scored by R, Y and S = 87 + 55 + 50 = 192
Total runs scored = 192/0.8 = 240
Runs scored by V (v3) and K (k3), v3, k3 < 50, v3+ k3? 48
R's M-index = 49
S's M-index = 50
V's M-index? 49
Y's M-index is either 40 or between 41 and 49.
S had the best M-index.
Hence, o
New answer posted
6 months agoContributor-Level 10
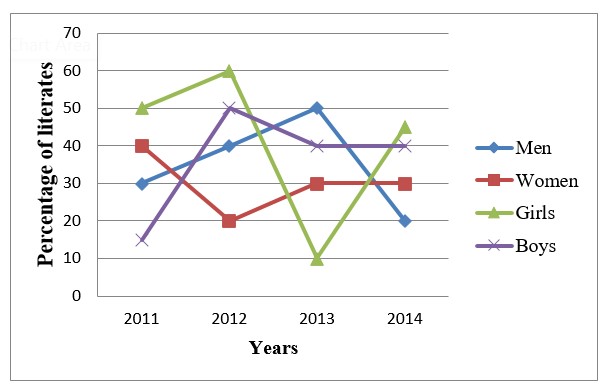
(c)
For 2011, the following table can be created.
| Population | Literacy Rate | No. of Literates |
Men | 20000 | 30% | 6000 |
Women | 13000 | 40% | 5200 |
Boys | 12000/ (1.5)3 | 15% | 1555 |
Girls | 10000/ (1.25)3 | 50% | 2560 |
Total |
|
| 15315 |
Hence, option 3.
New answer posted
6 months agoContributor-Level 10
(d)
In 2012, the population of women = 1.1 * 13000 and that of boys = 12000/ (1.05)2
Literacy rate of women and boys in 2012 is 20 percent and 50 percent respectively.
The ration of literate women to literate boys in 2012
Hence, option (d)
New answer posted
6 months agoContributor-Level 10
(c) rather than calculating for each year, we can deduce that since the number of men is significantly greater than the other three, the maximum number of literacy rate for men.
In 2003, the literacy rate for men is 50 percent, which is the highest for his category.
Considering that the number of men in the year 2013 is 40000, the number of literate men will be 20000 which is much higher as compared to the literate men in other years.
Hence, option (c)
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 687k Reviews
- 1800k Answers