Ncert Solutions Maths class 12th

Get insights from 2.5k questions on Ncert Solutions Maths class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Maths class 12th

2.5k
Questions
0
Discussions
0
Active Users
65
Followers

Have a question about Ncert Solutions Maths class 12th? Ask our experts

Ask Your Question

Keep it short & simple. Type complete word. Avoid abusive language.

New answer posted•a year ago

Ncert Solutions Maths class 12th Class 12th

$\underset{n \to \infty}{l i m} (1 + \frac{1 + \frac{1}{2} + . . . . . . . . . . + \frac{1}{n}}{n^{2}}) i s e q u a l t o :$

3 Views|Posted a year ago

Asked by Alok Kumar Singh

Answered by

Alok Kumar Singh | Contributor-Level 10

a year ago

$\underset{n \to \infty}{l i m} {(1 + \frac{1 + \frac{1}{2} + . . . . . . . + \frac{1}{n}}{n^{2}})}^{n}$ limit is in the form of $1^{\infty}$

$l = e x p (\underset{n \to \infty}{l i m} \frac{1 + \frac{1}{2} + \frac{1}{3} + . . . . . + \frac{1}{n}}{n^{2}})$

$0 \leq 1 + \frac{1}{2} + \frac{1}{3} + . . . . . + \frac{1}{n} \leq 1 + \frac{1}{\sqrt[]{2}} + \frac{1}{\sqrt[]{3}} + . . . . + \frac{1}{\sqrt[]{n}} \leq 2 \sqrt[]{n} - 1$

Taking limit $(n \to \infty)$

$l$ = exp (0) (from sandwich)

$l = 1$

Second Method :

1 + \frac{1}{2} + \frac{1}{3} + . . . . + \frac{1}{n} \geq l n (n + 1) . . . . . . . (i)

1 + \frac{1}{2} + \frac{1}{3} + . . . . . + \frac{1}{n} \leq 1 + \int_{1}^{2} \frac{1}{2} d x \leq 1 + l n n . . . . . . . . . . (i i)

From (i) & (ii)

$l n (n + 1) \leq 1 + \frac{1}{2} + \frac{1}{3} + . . . . + \frac{1}{n} \leq 1 + I n n, \forall n \in N, n \geq 2$ Views|Posted a year ago

Asked by Payal Gupta

Answered by

Payal Gupta | Contributor-Level 10

a year ago

$\vec{O} P = (2, - 1, 1)$

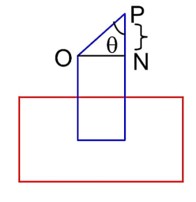
Normal vector to the plane

$= \vec{A} B \times A \vec{C} = | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & - 2 \\ 1 & 2 & - 1 \end{matrix} | = (3, - 1, 1) = \vec{n}$

Projection of $\vec{O} P o n \vec{n} i s | \frac{\vec{O} P . \vec{n}}{| \vec{n} |} |$

PN = $\frac{6 + 1 + 1}{\sqrt[]{11}} = \frac{8}{11}$

Projection of OP on plane = ON = $\sqrt[]{O P^{2} - P N^{2}} = \sqrt[]{6 - \frac{64}{11}} = \sqrt[]{\frac{2}{11}}$

Upvote

New answer posted•a year ago

Ncert Solutions Maths class 12th Class 12th

If the curves, $\frac{x^{2}}{a} + \frac{y^{2}}{b} = 1 a n d \frac{x^{2}}{c} + \frac{y^{2}}{d} = 1$ intersect each other at an angle of 90°, then which of the following relations is TRUE?

43 Views|Posted a year ago

Asked by Alok Kumar Singh

Answered by

Alok Kumar Singh | Contributor-Level 10

a year ago

$\frac{x^{2}}{a} + \frac{y^{2}}{b} = 1, \frac{x^{2}}{c} - \frac{y^{2}}{(- d)} = 1$

Ellipse and Hyperbola are orthogonal so these will be confocal.

$\sqrt[]{a - b} = \sqrt[]{c + (- d)}$

a – b = c – d

Upvote

New answer posted•a year ago

Ncert Solutions Maths class 12th Class 12th

The integral $\int \frac{e^{3 l o g_{e} 2 x} + 5 e^{2 l o g_{e} 2 x}}{e^{4 l o g_{e} x} + 5 e^{3 l o g_{e} x} - 7 e^{2 l o g_{e} x}} d x, x > 0 i s e q u a l t o :$ (where c is constant of integration)

6 Views|Posted a year ago

Asked by Payal Gupta

Answered by

Payal Gupta | Contributor-Level 10

a year ago

$l = \int \frac{8 x^{3} + 20 x^{2}}{x^{4} + 5 x^{3} - 7 x^{2}} d x = 4 \int \frac{2 x + 5}{x^{2} + 5 x - 7} d x = 4 l n | x^{2} + 5 x - 7 | + c$

Upvote

New answer posted•a year ago

Ncert Solutions Maths class 12th Class 12th

If Rolle’s theorm holds for the function f(x) = $x^{3} - a x^{2} + b x - 4, x \in [1, 2]$  with  $f' (\frac{4}{3}) = 0,$ then ordered pair (a, b) is equal to:

2 Views|Posted a year ago

Asked by Alok Kumar Singh

Answered by

Alok Kumar Singh | Contributor-Level 10

a year ago

$f (x) = x^{3} - a x^{2} + b x - 4$

f (1) = f (2)

->1 – a + b – 4 = 8 – 4a + 2b – 4

->3a – b = 7 . (i)

8a = 16 + 3b . (ii)

(i) and (ii) -> (a, b) = (5, 8)

Upvote

New answer posted•a year ago

Ncert Solutions Maths class 12th Class 12th

If a curve passes through the origin and the slope of the tangent to it at any point (x, y) is $\frac{x^{2} - 4 x + y + 8}{x - 2}$ , then this curve also passes through the point:

4 Views|Posted a year ago

Asked by Alok Kumar Singh

Answered by

Alok Kumar Singh | Contributor-Level 10

a year ago

As per questions

$\frac{d y}{d x} = \frac{x^{2} - 4 x + y + 8}{x - 2}$

$\frac{d y}{d x} = \frac{{(x - 2)}^{2} + (y + 4)}{(x - 2)}$

$\frac{d y}{d x} = (x - 2) + \frac{y + 4}{x - 2}$ .(i)

Let $\frac{y + 4}{x - 2} = t$

(y + 4) = t(x – 2)

Putting in equation (i)

$(x - 2) \frac{d t}{d x} + t = (x - 2) + t$ &nb

Upvote

New answer posted•a year ago

Ncert Solutions Maths class 12th Class 12th

If In = $\int_{\frac{π}{4}}^{\frac{π}{2}} c o t^{n} x d x, t h e n :$

2 Views|Posted a year ago

Asked by Payal Gupta

Answered by

Payal Gupta | Contributor-Level 10

a year ago

$l_{n} = \int_{π / 4}^{π / 2} c o t^{n} x d x = \int_{π / 4}^{π / 2} c o t^{n - 2} x (c o s e c^{2} x - 1) d x$

$= {[\frac{- c o t^{n - 1} x}{n - 1}]}_{π / 4}^{π / 2} - l_{n - 2} = \frac{1}{n - 1} - l_{n - 2}$

$l_{n} + l_{n - 2} = \frac{1}{n - 1}$

$\begin{array}{l} n = 4 \Rightarrow l_{4} + l_{2} = \frac{1}{3} \\ n = 5 \Rightarrow l_{5} + l_{3} = \frac{1}{4} \\ n = 6 \Rightarrow l_{6} + l_{4} = \frac{1}{5} \end{array}} \Rightarrow \frac{1}{l_{2} + l_{4}}, \frac{1}{l_{3} + l_{5}}, \frac{1}{l_{4} + l_{6}}$ are in A.P.

Upvote

New answer posted•a year ago

Ncert Solutions Maths class 12th Class 12th

Let $l = \frac{2 b^{2}}{a} = \frac{2 (1)}{3}$ be a twice differentiable function such that $\Rightarrow 9 (e^{2} + l)$ $= 9 (\frac{10}{9} + \frac{2}{3})$ , for all $= 10 + 6$ . If $= 16$ , then the value of $= \frac{10!}{5! 3! 2!} = 2520$ is

2 Views|Posted a year ago

Asked by Payal Gupta

Answered by

Payal Gupta | Contributor-Level 10

a year ago

$f : R \to R$

$(s i n ? x c o s ? y) (f (2 x + 2 y) - f (2 x - 2 y)) = (c o s ? x$ Put $s i n ? y) (f (2 x + 2 y) + f (2 x - 2 y))$

$x, y \in R$ Put $f^{'} (0) = \frac{1}{2}$

$24 f^{''} (\frac{5 π}{3})$

$(s i n ? x c o s ? y) (f (2 x + 2 y) - f (2 x - 2 y)) = (c o s ? x s i n ? y)$

$(f (2 x + 2 y) + f (2 x - 2 y))$

$f (2 x + 2 y) (s i n ? (x - y)) = f (2 x - 2 y) s i n ? (x + y)$

Upvote

New answer posted•a year ago

Ncert Solutions Maths class 12th Class 12th

Let A be a matrix of order $3 \times 3$ and $| A | = 5$ . If $| 2 a d j (3 A a d j (2 A)) | = 2^{α} \cdot 3^{β} \cdot 5^{γ} α, β, γ \in N$ then $α + β + γ$ is equal to

10 Views|Posted a year ago

Asked by Alok Kumar Singh

Answered by

Alok Kumar Singh | Contributor-Level 10

a year ago

: $? 2$ adj $(3 A$ adj(2A))|
${= 2}^{3} . ? 3 A$ adj(2A)| $|^{2}$

${= 2}^{3} \cdot {(3^{3})}^{2} \cdot | A |^{2} \cdot | a d j (2 A) |^{2}$ intersect the line $= 2^{3} \cdot 3^{6} \cdot | A |^{2} \cdot {(| 2 A |^{2})}^{2}$ at the point