Oscillations
Get insights from 99 questions on Oscillations, answered by students, alumni, and experts. You may also ask and answer any question you like about Oscillations
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New question posted
7 months agoNew answer posted
7 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
(d) For motion to be in SHM acceleration of the particle must be proportional to negative of displacement.

a , so y has to linear.
New answer posted
7 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
(b) y = sin3wt
= [3sinwt-4sin3wt]/4
dy/dt= [ ]/4
4dy/dt=3wcoswt-4 [3wcoswt]
4
= -
is not proportional to y. hence it is not SHM.
New answer posted
7 months agoContributor-Level 10
This is a multiple choice answer as classified in NCERT Exemplar
Velocity =dy/dt=
= 3 (-2w) [-sin ( )]
= 6wsin
Acceleration a = dv/dt=
= -4w2 [3cos ( )]
A = -4w2y hence acceleration is directly proportional to displacement so it follows SHM
w'= 2w
2
T'= 2 =
New answer posted
7 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
By considering the diagram
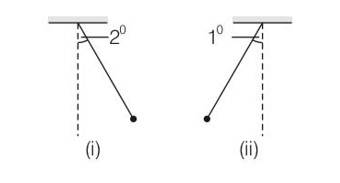
1=
2=
As it is clear given that amplitude time period being equal but phases being different. Now for first pendulum at any time t
1= 2
So sin = sin(wt+ )
wt+
where o=2o is the angular amplitude of first pendulum . for the second pendulum , the angular displacement is one degree , therefore 2= and negative sign is taken to show for being left to mean position.
-
Sin(wt+ )=-1/2
So (wt+ 2)=-
So by making their difference
(wt+ 2)-( 1)=7 =4
( 2- 1)= 1200
New answer posted
7 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
Consider the diagram of the spring block system. It is a SHM with amplitude of 5cm about the mean position
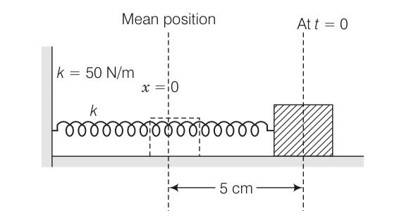
Spring constant k=50N/m
Mass =2kg
Angular frequency w=
Y (t)= Asin (wt+ )
Y (0)=Asin (w )
sin =1
y (t)=Asin (wt+ = Acoswt
A=5cm w=5rad/s
Y=5sin5t
New answer posted
7 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
given potential energy associated with the field
U (x)=Uo (1-cos )
F=-dU (x)/dx
F=-d (Uo-Uocos )=-Uo sin
F=-Uo
F
Motion is SHM for small oscillatons
F=-mw2X
Mw2=Uo
w2= , w=
T= =
New answer posted
7 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
Let us assume that the required displacement be x
Potential energy of the simple harmonic oscillator =1/2 kx2
k= force constant=mw2
PE= ½ mw2x2
Maximum energy of oscillator
TE= ½ mw2A2
PE=1/2 TE
½ mw2x2=
So x= =
New answer posted
7 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
As we know displacement y=sinwt-coswt
=
=
=
To comparing with standard equation
Y= asin (wt+ )
So T=2 /w
New answer posted
7 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
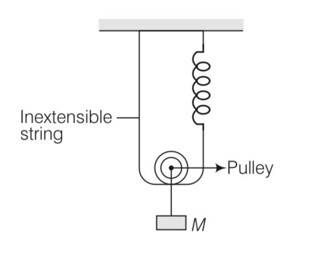
For calculation purpose, in this situation we will neglect gravity because it is constant throughout will not affect the net restoring force.
Let in the equilibrium position, the spring has extended by an amount xo
Let displacement by spring is and string be x .
But string is extensible so only spring will contribute in extension x+x=2x
So net extension is 2x+xo
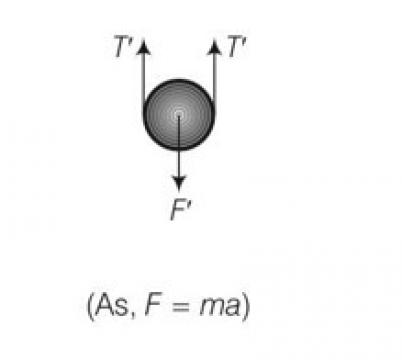
So force is F= 2T
T=kxo
F=2kxo
But when mass is lowered down further by x
F'=2T' but spring length is 2x+xo
F'=2k (2x+xo)
Restoring force on the system
Frestoring=- (F'-F)
So using above equations
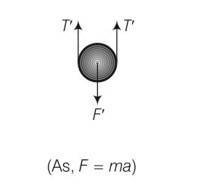
Frestoring= [2k (2x+x
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 686k Reviews
- 1800k Answers