Tags Oscillations

Oscillations

Get insights from 99 questions on Oscillations, answered by students, alumni, and experts. You may also ask and answer any question you like about Oscillations

Follow Ask Question

Questions

Discussions

Active Users

Followers

New answer posted

4 months ago

Oscillations Class 11th

A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that the log would execute S.H.M. with a time period. 2 m T A g π ρ = where m is mass of the body and ρ is density of the liquid.

0 Follower 2 Views

Payal Gupta

Contributor-Level 10

This is a long answer type question as classified in NCERT Exemplar

Let the log be passed and the vertical displacement at the vertical displacement at the equilibrium position

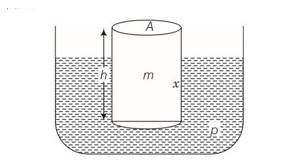
So mg= buoyant forces = $ρ A x_{o} g$

When it is displaced by further displacement x, the buoyant force is A (x_o+x) $ρ g$

Net restoring force = buoyant forces -weight

=A (x_o+x) $ρ g$ -mg

=A $ρ g x$

As displacement x is downward and restoring force is upward

F_restoring₌-A $ρ g x$ =-kx

So motion is SHM

Acceleration a=F_restoring/m=-kx/m

a=-w²x

w²=k/m

w= $\sqrt[]{\frac{k}{m}}$

T= 2 $π \sqrt[]{\frac{m}{k}} = 2 π \sqrt[]{\frac{m}{A ρ g}}$

0 0

New answer posted

4 months ago

Oscillations Class 11th

A body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4cm below the point, where it was held in hand. (a) What is the amplitude of oscillation? (b) Find the frequency of oscillation?

0 Follower 3 Views

Payal Gupta

Contributor-Level 10

This is a long answer type question as classified in NCERT Exemplar

(a) When the support of the hand is removed the body oscillates about mean position

Suppose x is the maximum extension in the spring when it reaches the lowest point in oscillation.

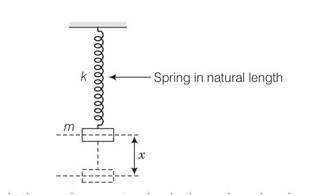
Loss in PE of the block=mgx

Gain in elastic potential energy =1/2 kx²

By energy conservation we cam say that

Mgx=1/2kx²

Or x= 2mg/k

Now the mean position of oscillation will be when the block is balanced by spring

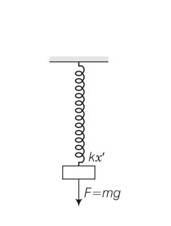
If x' is the extension in that case

F= kx'

F=mg

Mg=kx'

X'=mg/k

By dividing x by x'

x/x'= $\frac{2 m g / k}{m g / k} = 2$

so x=2x'

x'=4/2 =2cm

but the displacement of mass from the mean position when spring attains its natural l

...more

This is a long answer type question as classified in NCERT Exemplar

(a) When the support of the hand is removed the body oscillates about mean position

Suppose x is the maximum extension in the spring when it reaches the lowest point in oscillation.

Loss in PE of the block=mgx

Gain in elastic potential energy =1/2 kx²

By energy conservation we cam say that

Mgx=1/2kx²

Or x= 2mg/k

Now the mean position of oscillation will be when the block is balanced by spring

If x' is the extension in that case

F= kx'

F=mg

Mg=kx'

X'=mg/k

By dividing x by x'

x/x'= $\frac{2 m g / k}{m g / k} = 2$

so x=2x'

x'=4/2 =2cm

but the displacement of mass from the mean position when spring attains its natural length is equal to amplitude of the oscillation

A=x'=2cm

(b) Time period of the oscillating system depends on mass spring constant given by

T= $2 π \sqrt[]{\frac{m}{k}}$

2mg/k=x

2mg/k=4cm =4 $* 10^{- 2} m$

m/k =4 $* 10^{- 2}$ /2g

k/m=g/2 $* 10^{- 2}$

$v = \frac{1}{T} \sqrt[]{\frac{k}{m}}$

$v = \frac{1}{2 * 3.14} \sqrt[]{\frac{g}{2 * 10^{- 2}}}$

= $\frac{10}{628} * 2.21$ =3.51Hz

less

0 0

New answer posted

4 months ago

Oscillations Class 11th

A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s^-1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.

(a) Will there be any change in weight of the body, during the oscillation?

(b) If answer to part (a) is yes, what will be the maximum and minimum reading in the machine and at which position?

0 Follower 3 Views

Payal Gupta

Contributor-Level 10

This is a long answer type question as classified in NCERT Exemplar

(a) The weight of the body changes during oscillations.

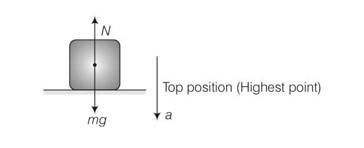
(b) Considering the situations in two extreme positions

we can say mg-N= ma

so at the highest point the platform is accelerating downward.

N=mg-ma

a=w²A

N=mg-mw²A

A= amplitude of motion m=50kg v=2m/s

w=2 $π v = 4 π r a d / s$

A= 5cm = 5 $* 10^{- 2} m$

N= 50 $* 9.8 - 50 * {(4 π)}^{2} * 5 * 10^{- 2} = 95.5 N$

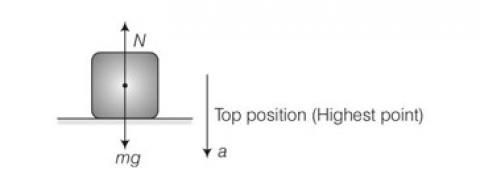
When it is accelerating towards mean position that is vertically upwards

N-mg=ma=Mw²A

N=mg+mw²A

N=m (g+w²A)

N= 50 [9.8+ ${(4 π)}^{2} * 5 * 10^{- 2}$ ]

N= 884N

Machine reads the normal reaction

Maximum weight =884N

Minimum weight=95.5N

0 0

New answer posted

5 months ago

Oscillations Class 11th

14.25 A mass attached to a spring is free to oscillate, with angular velocity $ω$ , in a horizontal plane without friction or damping. It is pulled to a distance $x_{0}$ and pushed towards the centre with a velocity $v_{0}$ at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters $ω, x_{0}$ and $v_{0}$ .

[Hint : Start with the equation x = a cos ( $ω$ t + $θ$ ) and note that the initial velocity is negative.]

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

The displacement equation for an oscillating mass is given by : x = Acos ( $ω t + θ)$ , where

A = the amplitude

x = the displacement

$θ = p h a s e c o n s t a n t$

Velocity, V = $\frac{d x}{d t}$ = -A $ω s i n ? (ω$ t + $θ)$

At t = 0, x = $x_{0}$ , $x_{0} = A \cos ? θ$ = $x_{0}$ ….(i)

And $\frac{d x}{d t}$ = $- v_{0}$ = A $ω \sin ? θ$ …….(ii)

Squaring and adding, we get

$A^{2} ({c o s}^{2} θ + {s i n}^{2} θ) = x_{0}^{2} + (\frac{v_{0}^{2}}{ω^{2}})$ , A = $\sqrt{x_{0}^{2} + ({\frac{v_{0}}{ω})}^{2}}$

0 0

New answer posted

5 months ago

Oscillations Class 11th

14.24 A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2 s. Find the acceleration and velocity of the body when the displacement is (a) 5 cm (b) 3 cm (c) 0 cm.

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

Amplitude = 5 cm = 0.05 m

Time period, T = 0.2 s

(a) For displacement x = 5 cm = 0.05m

Acceleration is given by a = ${- ω}^{2} x$ = $- ({\frac{2 π}{T})}^{2} x$ = $- ({\frac{2 π}{0.2})}^{2} * 0.05$ = $-$ 5 $π^{2}$ m/s

Velocity is given by V = $ω \sqrt{A^{2} - x^{2}}$ = $\frac{2 π}{T} \sqrt{{0.05}^{2} - {0.05}^{2}}$ = 0

(b) For displacement x = 3 cm = 0.03m

Acceleration is given by a = ${- ω}^{2} x$ = $- ({\frac{2 π}{T})}^{2} x$ = $- ({\frac{2 π}{0.2})}^{2} * 0.03$ = $-$ 3 $π^{2}$ m/s

Velocity is given by V = $ω \sqrt{A^{2} - x^{2}}$ = $\frac{2 π}{T} \sqrt{{0.05}^{2} - {0.03}^{2}}$ = 0.4 $π m / s$

(c) For displacement x = 0 cm = 0 m

Acceleration is given by a = ${- ω}^{2} x$ = $- ({\frac{2 π}{T})}^{2} x$ = $- ({\frac{2 π}{0.2})}^{2} * 0$ = $0$ m/s

Velocity is given by V = $ω \sqrt{A^{2} - x^{2}}$ = $\frac{2 π}{T} \sqrt{{0.05}^{2} 0}$ = 0.5 $π m / s$

0 0

New answer posted

5 months ago

Oscillations Class 11th

14.23 A circular disc of mass 10 kg is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5 s. The radius of the disc is 15 cm. Determine the torsional spring constant of the wire. (Torsional spring constant $α$ is defined by the relation J = – $α θ$ , where J is the restoring couple and $θ$ the angle of twist).

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

Mass of the circular disc, m = 10 kg

Radius of the disc, r = 15 cm = 0.15 m

The torsional oscillation of the disc have a time period, T = 1.5 s

The moment of inertia of the disc I = $\frac{1}{2}$ m $r^{2}$ = $\frac{1}{2} * 10 * {0.15}^{2} \frac{k g}{m^{2}}$ = 0.1125 $\frac{k g}{m^{2}}$

Time period, T = 2 $? \sqrt{\frac{I}{?}}$ ,

Torsional spring constant, $? = \frac{4 ?^{2} I}{T^{2}} = \frac{4 {* ?}^{2} * 0.1125}{{1.5}^{2}}$ = 1.974 Nm/rad

0 0

New answer posted

5 months ago

Oscillations Class 11th

14.22 Show that for a particle in linear SHM the average kinetic energy over a period of oscillation equals the average potential energy over the same period.

0 Follower 3 Views

Vishal Baghel

Contributor-Level 10

The equation of displacement of a particle executing SHM at an instant t is given bas:

x = Asin $ω t$ , where A = Amplitude of oscillation and $ω$ = angular frequency = $\sqrt{\frac{k}{M}}$

The velocity of the particle, v = $\frac{d x}{d t}$ = A $ω \cos ? ω t$

The kinetic energy of the particle $E_{k}$ = $\frac{1}{2}$ M $v^{2}$ = $\frac{1}{2}$ M ${(A ω \cos ? ω t)}^{2}$ = $\frac{1}{2}$ M $A^{2} ω^{2} {c o s}^{2} ω t$

The potential energy of the particle $E_{p}$ = $\frac{1}{2}$ k $x^{2}$ = $\frac{1}{2}$ k $A^{2} {s i n}^{2} ω t$

For time period T, the average kinetic energy over a single cycle is given as :

${E_{k}}_{a v g} = \frac{1}{T} \int_{0}^{T} E_{k} d t$ = $\frac{1}{T} \int_{0}^{T} \frac{1}{2} M A^{2} ω^{2} {c o s}^{2} ω t d t$ = $\frac{M A^{2} ω^{2}}{2 T} \int_{0}^{T} {c o s}^{2} ω t d t$

= $\frac{M A^{2} ω^{2}}{2 T} \int_{0}^{T} \frac{(1 - c o s 2 ω t)}{2} d t$ = $\frac{M A^{2} ω^{2}}{2 T} ({t + \frac{s i n 2 ω t}{2 ω})}_{0}^{T}$ = $\frac{M A^{2} ω^{2}}{4 T} (T)$ = $\frac{1}{4} M A^{2} ω^{2}$ …….(i)

Average potential energy

...more

The equation of displacement of a particle executing SHM at an instant t is given bas:

x = Asin $ω t$ , where A = Amplitude of oscillation and $ω$ = angular frequency = $\sqrt{\frac{k}{M}}$

The velocity of the particle, v = $\frac{d x}{d t}$ = A $ω \cos ? ω t$

The kinetic energy of the particle $E_{k}$ = $\frac{1}{2}$ M $v^{2}$ = $\frac{1}{2}$ M ${(A ω \cos ? ω t)}^{2}$ = $\frac{1}{2}$ M $A^{2} ω^{2} {c o s}^{2} ω t$

The potential energy of the particle $E_{p}$ = $\frac{1}{2}$ k $x^{2}$ = $\frac{1}{2}$ k $A^{2} {s i n}^{2} ω t$

For time period T, the average kinetic energy over a single cycle is given as :

${E_{k}}_{a v g} = \frac{1}{T} \int_{0}^{T} E_{k} d t$ = $\frac{1}{T} \int_{0}^{T} \frac{1}{2} M A^{2} ω^{2} {c o s}^{2} ω t d t$ = $\frac{M A^{2} ω^{2}}{2 T} \int_{0}^{T} {c o s}^{2} ω t d t$

Average potential energy over one cycle is given as :

${E_{p}}_{a v g} = \frac{1}{T} \int_{0}^{T} E_{p} d t$ = $\frac{1}{T} \int_{0}^{T} \frac{1}{2} M A^{2} ω^{2} \sin ? ω t d t$

= $\frac{M A^{2} ω^{2}}{2 T} \int_{0}^{T} \frac{(1 - c o s 2 ω t)}{2} d t$ = $\frac{M A^{2} ω^{2}}{2 T} ({t - \frac{s i n 2 ω t}{2 ω})}_{0}^{T}$ = $\frac{M A^{2} ω^{2}}{4 T} (T)$ = $\frac{1}{4} M A^{2} ω^{2}$ …….(ii)

From equations (i) and (ii), it is proved that average kinetic energy for a given period of time is equal to the average potential energy for the same period of time.

less

0 0

New answer posted

5 months ago

Oscillations Class 11th

14.21 You are riding in an automobile of mass 3000 kg. Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags 15 cm when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by 50% during one complete oscillation.

Estimate the values of

(a) The spring constant k and

(b) The damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports 750 kg.

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

Mass of the automobile, m = 3000 kg

Displacement of the suspension system, x = 15 cm = 0.15 m

There are 4 springs in parallel to the support of the mass of the automobile.

(a) The equation for restoring force for the system, F = -4kx = mg, where k is the spring constant of the suspension system

Time period, T = 2 $π \sqrt{\frac{m}{k}}$ and

k = $\frac{m g}{4 x}$ = $\frac{3000 * 9.8}{4 * 0.15} = 4.9 * 10^{4}$ N/m

(b) Each wheel supports a mass, M = 3000/4 = 750 kg

For damping factor b, the equation for displacement is written as

x = $x_{0} e^{- b t / 2 M}$

The amplitude of oscillation decrease by 50%. Therefore x = $\frac{x_{0}}{2}$ = $x_{0} e^{- b T / 2 M}$

$\log_{e} ? 2$ = $\frac{b T}{2 M}$

b = $\frac{2 M \log_{e} ? 2}{T}$

T = 2 $π \sqrt{\frac{m}{4 k}}$ = 2 $π \sqrt{\frac{3000}{4 * 4.9 * 10^{4}}}$ = 0.7773 s

b = $\frac{2 * 750 * 0.693}{0.7773}$

...more

Mass of the automobile, m = 3000 kg

Displacement of the suspension system, x = 15 cm = 0.15 m

There are 4 springs in parallel to the support of the mass of the automobile.

(a) The equation for restoring force for the system, F = -4kx = mg, where k is the spring constant of the suspension system

Time period, T = 2 $π \sqrt{\frac{m}{k}}$ and

k = $\frac{m g}{4 x}$ = $\frac{3000 * 9.8}{4 * 0.15} = 4.9 * 10^{4}$ N/m

(b) Each wheel supports a mass, M = 3000/4 = 750 kg

For damping factor b, the equation for displacement is written as

x = $x_{0} e^{- b t / 2 M}$

The amplitude of oscillation decrease by 50%. Therefore x = $\frac{x_{0}}{2}$ = $x_{0} e^{- b T / 2 M}$

$\log_{e} ? 2$ = $\frac{b T}{2 M}$

b = $\frac{2 M \log_{e} ? 2}{T}$

T = 2 $π \sqrt{\frac{m}{4 k}}$ = 2 $π \sqrt{\frac{3000}{4 * 4.9 * 10^{4}}}$ = 0.7773 s

b = $\frac{2 * 750 * 0.693}{0.7773}$ = 1337.32 kg/s

Therefore the damping constant of the spring is 1337.32 kg/s

less

0 0

New answer posted

5 months ago

Oscillations Class 11th

14.20 An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

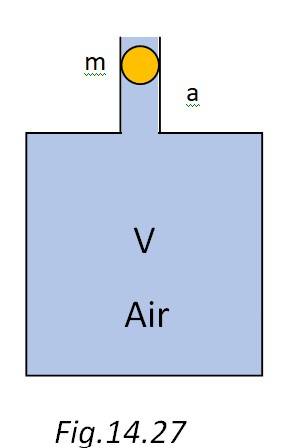
Volume of the air chamber = V

Area of cross-section of the neck = a

Mass of the ball = m

The pressure inside the chamber is equal to atmospheric pressure.

Let the ball be depressed by x units. As a result of depression, there would be decrease in volume and an increase of pressure inside the cylinder.

Decrease in the volume, $? V$ = ax

Volumetric strain = $\frac{? V}{V}$ = $\frac{a x}{V}$

Bulk modulus of air, B = $\frac{S t r e s s}{S t r a i n}$ = $\frac{- p}{\frac{a x}{V}}$ : here stress is the increase in pressure. The negative sign indicates that pressure increases with a decrease in volume.

So p = $- \frac{B a x}{V}$

The restoring force acting on the ball, F = p $* a$ = $- \frac{B a^{2} x}{V}$ …. (i)

In SHM,

...more

Volume of the air chamber = V

Area of cross-section of the neck = a

Mass of the ball = m

The pressure inside the chamber is equal to atmospheric pressure.

Let the ball be depressed by x units. As a result of depression, there would be decrease in volume and an increase of pressure inside the cylinder.

Decrease in the volume, $? V$ = ax

Volumetric strain = $\frac{? V}{V}$ = $\frac{a x}{V}$

So p = $- \frac{B a x}{V}$

The restoring force acting on the ball, F = p $* a$ = $- \frac{B a^{2} x}{V}$ …. (i)

In SHM, the equation of restoring force, F = -kx …. (ii)

Combining equation (i) and (ii), we get k = $\frac{B a^{2}}{V}$

Time period, T = 2 $π \sqrt{\frac{m}{k}}$ = 2 $π \sqrt{\frac{V m}{B a^{2}}}$

less

0 0

New answer posted

5 months ago

Oscillations Class 11th

14.19 One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

Area of cross section of the U tube = A

Density of the mercury column = $ρ$

Acceleration due to gravity = g

Restoring force, F = Weight of the mercury column of a certain height = - (Volume $* d e n s i t y * g)$

F = -(A $* 2 h * ρ * g)$ = -2A $ρ g$ = -k $* d i s p l a c e m e n t i n o n e o f t h e a r m s (h)$

Where, 2h is the height of the mercury columns in two arms

The constant k is given by k = $- \frac{F}{h}$ = 2A $ρ g$

Time period, T = 2 $π \sqrt{\frac{m}{k}}$ = 2 $π \sqrt{\frac{m}{2 A ρ g}}$ , where m is the mass of the mercury column

Let l be the length of the total mercury in the U tube

Mass of the mercury, m = Volume of the mercury $*$ density of mercury = Al $ρ$

Hence T = 2 $π \sqrt{\frac{A l ρ}{2 A ρ g}}$ = 2 $π \sqrt{\frac{l}{2 g}}$

0 0

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
686k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Need guidance on career and education? Ask our experts

Your Question

Oscillations

Questions

Discussions

Active Users

Followers

All

Discussions

Unanswered Questions

Share Your College Life Experience