Oscillations
Get insights from 99 questions on Oscillations, answered by students, alumni, and experts. You may also ask and answer any question you like about Oscillations
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Base area of the cork = A
Height of the cork = h
Density of the liquid =
Density of the cork =
In equilibrium, Weight of the cork = Weight of the liquid displaced by the floating cork
Let the cork be depressed slightly by an amount x, as a result, some extra water of a certain volume is displaced. Hence, an extra up-thrust acts upward and provides restoring force to the cork.
Up-thrust (Restoring force) = weight of the extra water displaced
F = mg =
Volume = Area distance through which the cork is depressed
V = Ax
F = A ….(i)
According to force law, F= kx, where k is constant
k = = A
New answer posted
7 months agoContributor-Level 10
The bob of the simple pendulum will experience the acceleration due to gravity and the centripetal acceleration provided by the circular motion of the car.
Acceleration due to gravity = g
Centripetal acceleration = , where v is the uniform speed of the car and R is radius of the track.
Effective acceleration is given by
Time period, T = 2 , where l = length of the pendulum
New answer posted
7 months agoContributor-Level 10
(a) The time period of a simple pendulum, T = 2
For a simple pendulum, k is expressed in terms of mass, m as : k or = constant
Hence, the time period of a simple pendulum is independent of the mass of the bob. In the case of a simple pendulum, the restoring force acting on bob is given as F = -mg , where
F = restoring force
m = mass of the bob
g = acceleration due to gravity
(b) For small sin . For larger sin is greater than . This decreases the effective value of g.
Hence the time period increase as : T = 2 , where l is the length of
New answer posted
7 months agoContributor-Level 10
Acceleration due to gravity on Moon surface, g' = 1.7 m/
Acceleration due to gravity on Earth surface, g = 9.8 m/
Time period on Earth, T = 3.5 s
We know T = 2 where l = length of the pendulum
l = = = 3.041 m
On Moon surface, the length of the pendulum remained same = 3.041 m
So time period on moon surface, T' = 2 = 2 = 8.40 s
New answer posted
7 months agoContributor-Level 10
Angular frequency of the piston,
Stroke = 1 m
Amplitude, A = Stroke/2 = 0.5 m
The maximum piston speed, A = 200 = 100 m/min
New answer posted
7 months agoContributor-Level 10
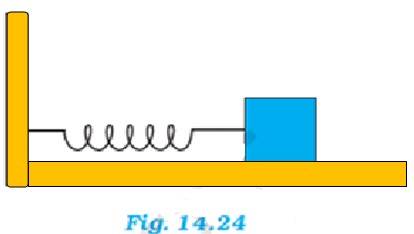
(a) For figure (a) : When a force F is applied to the free end of the spring, an extension l is produced. For the maximum extension, it can be written as:
F – kl, where k is the spring constant.
For maximum =extension of the spring, l =
For figure (b): The displacement (x) produced in this case is x =
Net force F = +2kx = 2k . So l =
(b) For figure (a) : For mass (m) of the block, force is written as : F = ma = m ,
where x is the displacement of the block in time t, then
m , it is negative because the direction of the elastic force is opposite to the direction of displacement.
=&
New answer posted
7 months agoContributor-Level 10
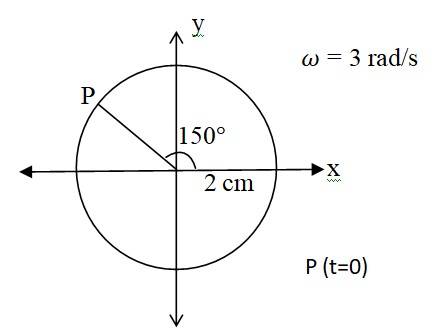
(a) X = -2 sin( 3t + ) = +2cos ( 3t + + = 2 cos (3t + )
when we compare this equation with standard SHM equation
x = Acos ( t + ), then we get
Amplitude A = 2 cm. Phase angle = 150 , angular velocity = 3 rad/s
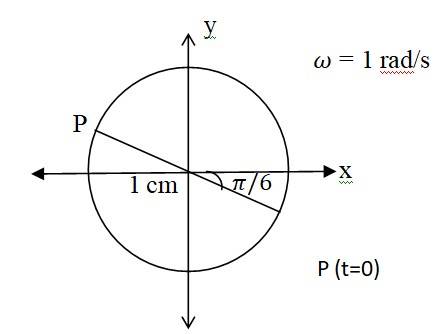
(b) X= cos ( t) = cos ( )
when we compare this equation with standard SHM equation
x = Acos( t + ), then we get
Amplitude A = 1 cm. Phase angle = - 30 , angular velocity = 1 rad/s
(c) X = 3sin (2 t + ) = -3cos
when we compare this equation w
New answer posted
7 months agoContributor-Level 10
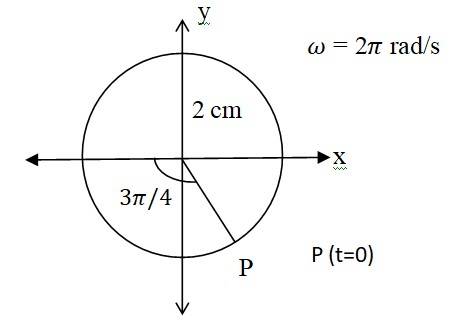
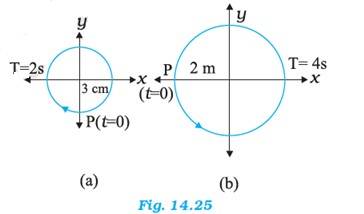
(a) Time period, T = 2 s, Amplitude A = 3 cm
At time, t = 0, the radius vector makes an angle with the positive x-axis, i.e. phase angle = +
Therefore, the equation of simple harmonic motion for the x-projection of the radius vector, at time t is given by the displacement equation:
x = Acos = 3cos = -3sin ( ) = -3sin cm
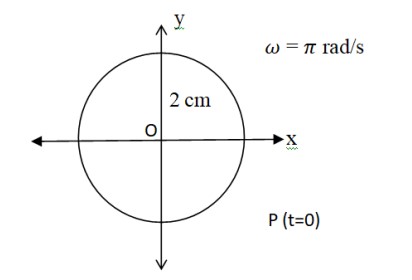
(b) Time period, T = 4 s, Amplitude A = 2 m
At time, t = 0, the radius vector makes an angle with the positive x-axis, i.e. phase angle = +
Therefore, the equation of simple harmonic motion for the x-projection of the r
New answer posted
7 months agoContributor-Level 10
The functions have the same frequency and amplitude, but different initial phases.
Distance travelled by the mass sideways, A = 2.0 cm
Force constant of the spring, k = 1200 N/m and mass, m = 3 kg
Angular frequency, = = 20 rad/s
(a) When mass is at the mean position, displacement x = Asin cm
(b) At the maximum stretched position, the mass is towards extreme right. Hence the initial phase is
x = A sin ( = 2sin (20t + = 2cos20t
(c) At the maximum compressed position, the mass is towards the extreme left
Hence, the initial phase is
x = Asin ( = 2 cos20t
Hence, the f
New answer posted
7 months agoContributor-Level 10
Spring constant, k = 1200 N/m
Mass, m = 3 kg
Displacement, d = 2 cm = 0.02 m
(a) Frequency of oscillation, v is given by
v = = = = 3.183 m/s
(b) Maximum acceleration (a) is given by the relation: a =
where, angular frequency = and A = maximum displacement
a = = = 8 m/
(c) Maximum velocity, = = 0.4 m/s
Hence the maximum velocity of the mass is 0.4 m/s
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 680k Reviews
- 1800k Answers