Systems of Particles and Rotational Motion
Get insights from 31 questions on Systems of Particles and Rotational Motion, answered by students, alumni, and experts. You may also ask and answer any question you like about Systems of Particles and Rotational Motion
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
5 months agoContributor-Level 10
Case – I : When disk slides down
Case – II : When disk rolls down
New answer posted
7 months agoContributor-Level 10
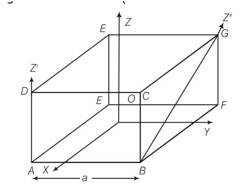
This is a multiple choice type question as classified in NCERT Exemplar
a, b, d
a) according to the perpendicular axes theorem statement 1 is wrong
b) As z'|z so distance between them = a
So according to parallel axes theorem Iz'=Iz+m (a/ )2= Iz+ma2/2
Hence b is true
c) z' is not parallel to z hence Parallel axes does not applied so statement is false
d) as x and y axes are symmetrical . hence Ix=Iy so d is true
d) as x and y axes are symmetrical . hence Ix=Iy so d is true
New answer posted
7 months agoContributor-Level 10
This is a multiple choice type question as classified in NCERT Exemplar
b, c
a) When r>r'
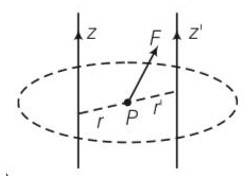
Torque about z-axis t=r F
b) t'=r' which is along negative z axis
c) tz=Fr = magnitude of torque about z axis where r is perpendicular between F and z axis so torque along positive z axis is greater than negative z axis.
d) We are always calculating resultant torque about common axis. Hence total torque not equal to combination of torque along both axis of z, because they are not on common axis.
New answer posted
7 months agoContributor-Level 10
This is a multiple choice type question as classified in NCERT Exemplar
a, b, c, d
As we know torque = r F = rFsin
a) when forces act radially angle =0 hence torque =0
b) when forces are acting on the axis of rotation r=0 torque=0
c) when forces acting parallel to the axis of rotation angle =0 so torque =0
d) when torque by forces are equal and opposite torque net = t1-t2=0
New answer posted
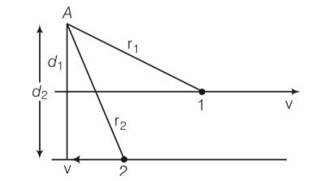
7 months agoContributor-Level 10
This is a multiple choice type question as classified in NCERT Exemplar
(a), (b)As we know L= r p where r is position vector and p is the linear momentum . the direction of L is perpendicular to both r and p by right hand rule.
For particle 1
I1=r1 mv is out of the plane of the paper and perpendicular to r1 and p . similarly I2=r2 m (-v) is into the plane of the paper and perpendicular to r2 and -p.
Hence total angular momentum
L= L1+L2= I1=r1 mv+ (r2 m (-v)
L= mvd1-mvd2 as d2>d1
So total angular momentum will be inwards so I = l = mv (d2-d1)⊗
L= mvd1-mvd2 as d2>d1
So total angular momentum will be inwards so I = l = mv (d2-d1)?
New answer posted
7 months agoContributor-Level 10
This is a multiple choice type question as classified in NCERT Exemplar
(a), (c) For general rotational motion where axis of rotation is not symmetric . angular momentum L and angular velocity w need not be parallel. For general translational motion momentum p=mv hence p and v are always parallel.
New answer posted
7 months agoContributor-Level 10
This is a multiple choice type question as classified in NCERT Exemplar
(a) As no external torque acts on the system, angular momentum should be conserved hence Iw=constant
Where I is moment of inertia of the system and w is the angular velocity of the system.
So I1w1= I2w2
Where w1 and w2 are angular velocities before and after jumping.
Iw=
w2=2w
New answer posted
7 months agoContributor-Level 10
This is a multiple choice type question as classified in NCERT Exemplar
(a) Density is given as ρ (x) = a (1+bx2)
Where a and b are constant and 0
Let b=0 ρ (x) = a= constant
Hence COM will be at x =0.5m
Putting b=0 ain above option only a gives this answer.
We should not check options by putting a=0 because for a=0
New answer posted
7 months agoContributor-Level 10
This is a multiple choice type question as classified in NCERT Exemplar
(c) First the centre of mass of the system was on the dotted line and was shifted towards Q from the centre. When mass is removed it will be on the same line but shifed away from the centre and below 3rd quadrant.

Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers