Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Step I: Calculation of energy required
ΔE = E∞– E2
= 0 – (–2.18 * 10-18 J) / 4 = 5.45 x 10-19 J
Step II: Calculation of the longest wavelength of light in cm used to cause the transition
λ = hc / ΔE = (6.626 x 10-34 J s) x (3 x 108 ms-1) / (5.45 x 10-19 J)
= 3.644 x 10-7 x 102 = 3.645 x 10-5 cm.
New answer posted
7 months agoContributor-Level 10
Step I: calculation of energy required
Energy of electron (En) = (- 2.18 x 10-11ergs) / n2= (- 2.18 x 10-18 J) / n2
Energy in Bohr's 1st orbit (E1) = (- 2.18 x 10-18 J) / 12
Energy in Bohr's 5th orbit (E1) = (- 2.18 x 10-18 J) / 52
Therefore, energy required (ΔE) = E5 – E1 = [ (- 2.18 x 10-18 J) / 25] – [ (- 2.18 x 10-18 J) / 1]
= 2.18 x 10-18 (1 – 1/25) J
= 2.18 x 10-18 x 24 / 25
= 2.09 x 10-18 J
Step II: Calculation of wavelength of light emitted
λ = hc / ΔE = (6.626 x 10-34 J s) x (3 x 108 ms-1) / (2.09 x 10-18 J) = 9.50 x 10-8 m = 950
New answer posted
7 months agoContributor-Level 10
According to Balmer formula? = 1 / λ = RH [1/n12 – 1/n22]
For the longest wavelength transition in the Balmer series of atomic hydrogen, wave number must be least. This is possible in case n2 – n1 = minimum; i.e. n1 = 2 and n2 = 3. Substituting the values:
? = 1 / λ = (1.097 x 107 m-1) [1/22 – 1/32] = (1.097 x 107 m-1) [5/36] = 1.523 x 106 m-1
New answer posted
7 months agoContributor-Level 10
(i) For an electron, the energies in the two orbits can be compared as:
E1 / E2 = (n2 / n1)2 [Since E is inversely proportional to n2]
Given: n1 = 1, E1 = –2.17 * 10-18 J atom-1, n2 = 5
Therefore, (–2.17 * 10-18 J atom-1) / E2 = (5 / 1) 2 = 25
=> E2 = (–2.17 * 10-18 J atom-1) / 25 = –8.77 x 10-20 J atom-1
(ii) For hydrogen atom; rn = 0.529 x n2 Å
r5 = 0.529 x (5)2 = 13.225 Å = 1.3225 nm.
New answer posted
7 months agoContributor-Level 10
The maximum no. of emission lines = [n (n–1)] /2 = [6 (6–1)] / 2 =3 * 5 = 15
The transitions that take place are as follows:
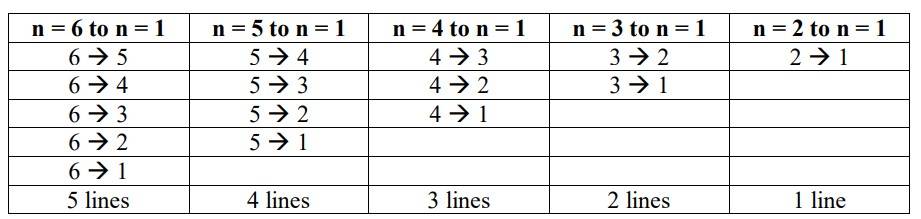
New answer posted
7 months agoContributor-Level 10
Energy of a hydrogen present in a particular energy shell,
En = 13.12 x 105 / n2 J mol-1 = (13.12 x 105) / (n2 x 6. 022 x 1023) J atom-1
= -2.18 x 10-18 / n2 J atom-1
Step I: Ionisation energy for hydrogen electron present in orbit n = 5
IE5 = E∞ - E5 = 0 – [ (-2.18 x 10-18) / 25] J atom-1 = 8.72 x 10-20 J atom-1
Step II: Ionisation energy for hydrogen electron present in orbit n = 1
IE1 = E∞ - E1 = 0 – [ (-2.18 x 10-18) / 1] J atom-1 = 2.18 x 10-18 J atom-1
Therefore IE1 / IE5 = (2.18 x 10-18 J atom-1) / (8.72 x 10-20 J atom-1) = 25
The energy required to remove an electron from first orbit in a hydrogen atom is 25 times the energy n
New answer posted
7 months agoContributor-Level 10
According to Balmer formula,
Wave number (? ) = RH [1/n12 - 1/n22 ]cm-1
= 109678 [1/22 – 1/42] cm-1
= (109678 x 3) / 16 cm-1
λ = 1 /? = 16 / (109678 x 3) cm = 16 x 107 / (109678 x 3) nm = 486 nm
New answer posted
7 months agoContributor-Level 10
Threshold frequency (v0) = c /λ = (3 * 108 m s-1) / (68 x 10-8 m) = 4.41 x 1014 s-1
Work function (W0) = hv0 = (6.626 * 10-34 Js) x (4.41 x 1014 s-1) = 2.92 x 10-19 J.
New answer posted
7 months agoContributor-Level 10
Energy of one photon (E) = hc / λ
= (6.626 * 10-34 Js) x (3 * 108 m s-1) / (0.57 * 10-6 m) = 3.48 x 10-19 J
Rate of emission of quanta per second = Power / Energy = (25 watt) / (3.48 x 10-19 J)
= (25 Js-1) / (3.48 x 10-19 J) = 7.18 x 1019 s-1
New answer posted
7 months agoContributor-Level 10
Given: λ = 242 nm = 142 x 10-9 m, c = 3 x 108 ms-1, h = 6.626 x 10-34Js
We know, E = hc / λ
= (6.626 * 10-34 Js) x (3 * 108 m s-1) / (242 * 10-9 m) = 0.0821 x 10-17 J
∴ Ionization energy per mol (E) = (0.0821 x 10-17 J) x (6.022 x 1023 mol-1J) / 1000 = 494 kJ mol-1
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
