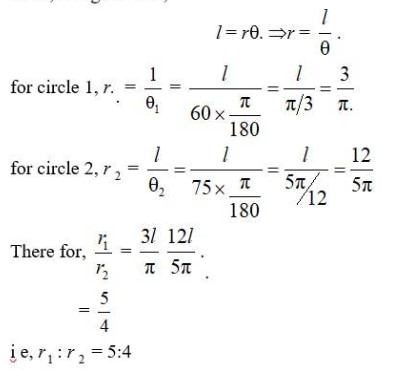Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
42. The given system of inequality is
x+y≤ 6 - (1)
x+y≥ 4- (2)
So the corresponding equations are
x+y=6
x | 0 | 6 |
y | 6 | 0 |
and x + y = 4
x | 4 | 0 |
y | 0 | 4 |
Putting (x, y)= (0,0) in equality (1) and (2),
0+0 ≤ 6 and 0 + 0 ≥ 4
0 ≤ 6 is true. => 0 ≥ 4 is false.
So, solution of plane of inequality (1) includes the origin and inequality (2) does not includes the origin.
? The reqd solution of the given system of inequality is the shaded region.
New answer posted
7 months agoContributor-Level 10
41. The given system of inequality is
2x – y> 1 - (1)
x – 2y< 1- (1)
So the corresponding equations are
2x – y=1
x | 0 | 0.5 |
y | –1 | 0 |
and x – 2y= –1
x | –1 | 0 |
y | 0 | 0.5 |
Putting (x, y)= (0,0) in (1) and (2) to cheek the inequality
2 * 0 – 0 > 1
0 > 1 which is not true.
and 0 – 2 * 0< 1
0< 1 which is not true.
So, the solution of plane of inequality (1)and (2) does not include the plane with point (0,0) or origin.
? The reqd. solution of the given system of inequality is the shaded region.
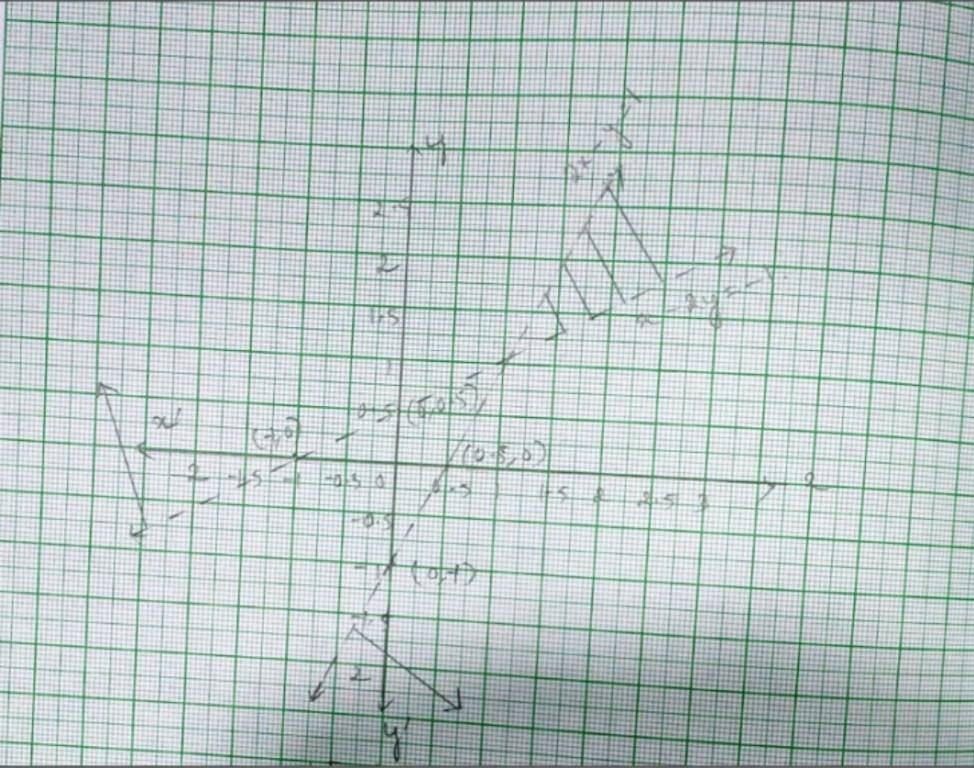
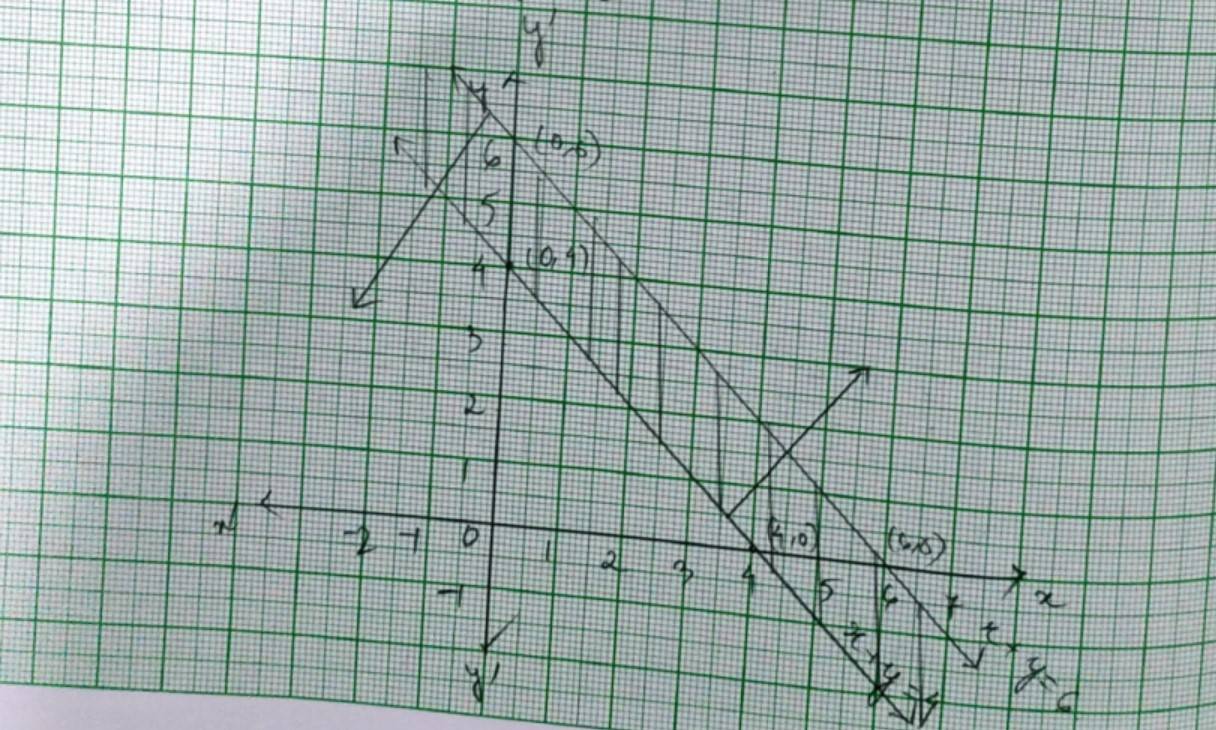
New answer posted
7 months agoContributor-Level 10
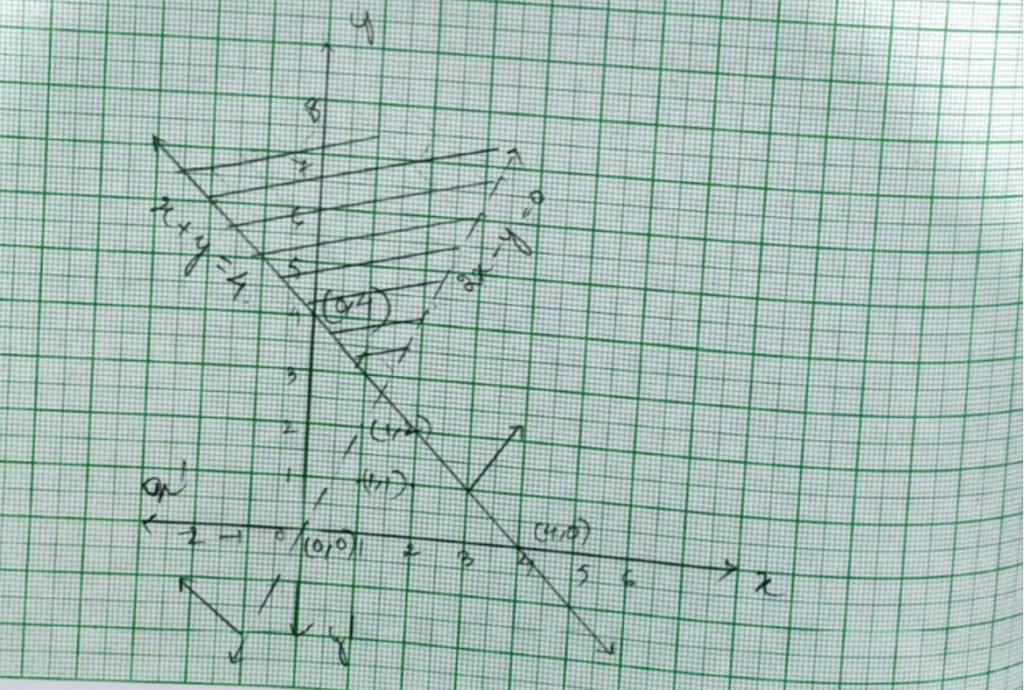
40. The given system of inequalities is
x + y ≥ 4.- (1)
2x – y< 0.- (2)
The corresponding equations are x+y=4 and 2x – y=0.
x | 0 | 4 |
y | 4 | 0 |
and
X | 0 | 1 |
Y | 0 | 2 |
Put (x, y)= (1,1) in (1) and (2).
So, 1+1 ≥ 4
2 ≥ 4 which is not true.
and 2 * 1 – 1<0
1<0 which is not true.
So solution of plane of inequality (1) and (2) does not include the plane with point (1,1).
? The reqd. solution of the given system of inequality is the shaded portion.
New answer posted
7 months agoContributor-Level 10
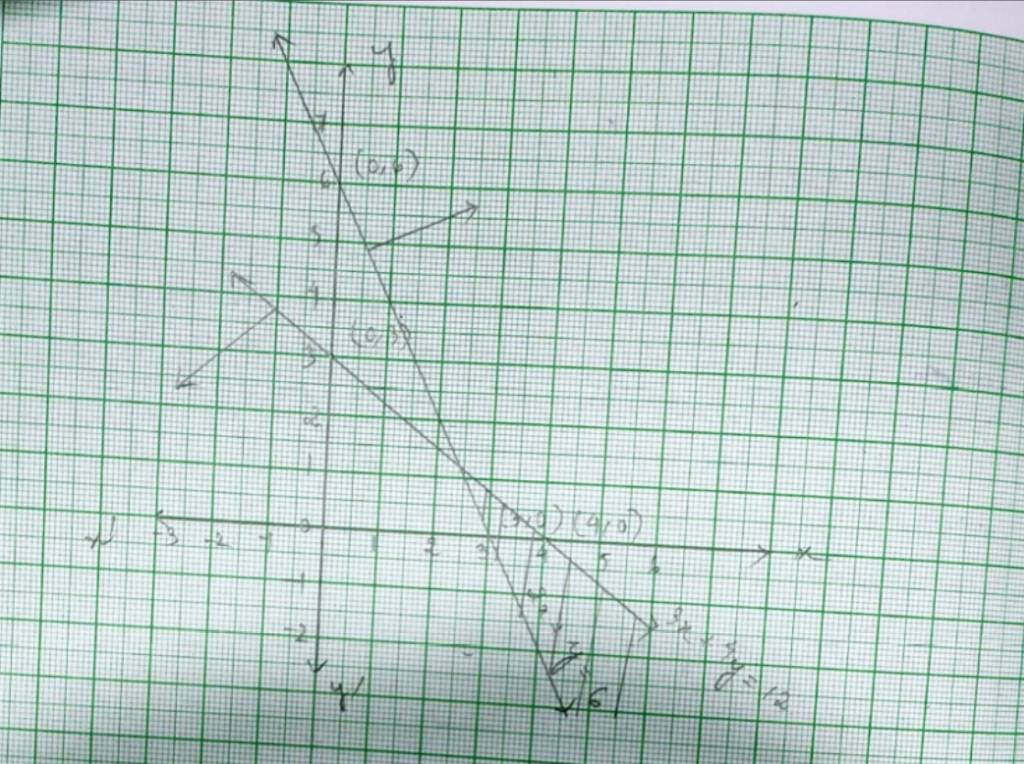
39.The given system of inequalities is
2x+y ≥ 6 - (1)
3x+4y ≤ 12- (2)
The corresponding equations are
2x + y = 6
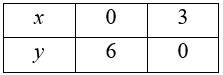
and 3x + 4y = 6
So,
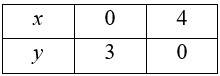
Put (x, y)= (0,0) in (1), (2),
? 2 * 0+0 ≥ 6
0 ≥ 6 which is false.
And 3 * 0+4 * 0 ≤ 12
0 ≤ 12 which is true.
So, solution of inequality (1) lies on the plane which excludes the origin and the solution of inequality (2) lies on
New answer posted
7 months agoContributor-Level 10
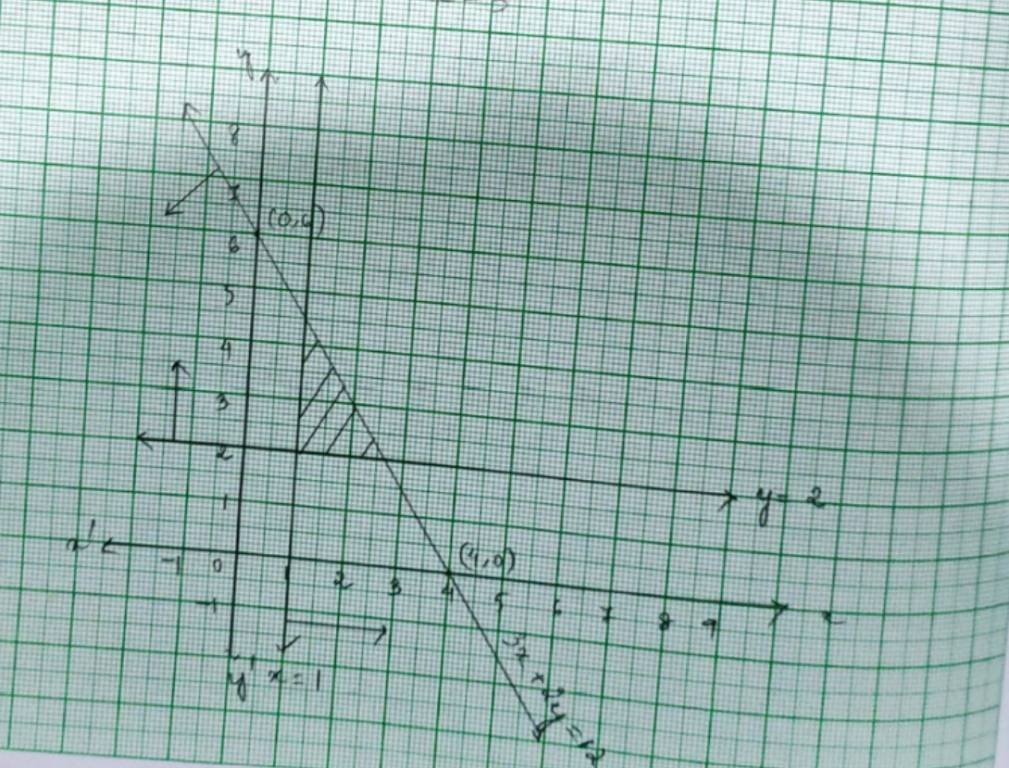
38.
2. The given system of inequalities are
3x+2y≤ 12- (1)
x≥ 1- (2)
y≥ 2- (3)
We draws the graphs of the lines 3x+2y=12 using points and as 3 * 0 + 2 * 0 ≤ 12
The solution is plane which includes the origin (0, 0).
0 ≤ 12
and x = 1 and y = 2.
The inequality (1), (2) and (3) represents the region between these three lines including the points on the respective lines. So, every point on the shaded region in first quadrant represents a solution of the given system of inequalities.
New answer posted
7 months agoContributor-Level 10
7. Here,
r= length of pendulum.
r= 75 cm.
(i) Arc of length, l = 10 cm
Ø= = radian.
(ii) Arc of length, l = 15 cm.
So, Ø= = radian.
(iii) Arc for length, l= 21 cm.
So, Ø= radian.
New answer posted
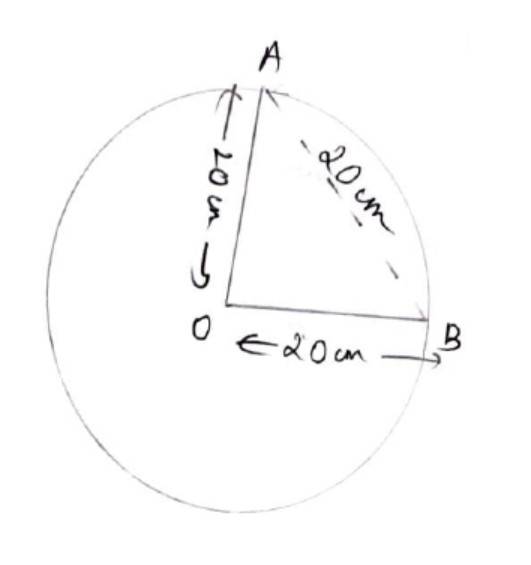
7 months agoNew answer posted
7 months agoContributor-Level 10
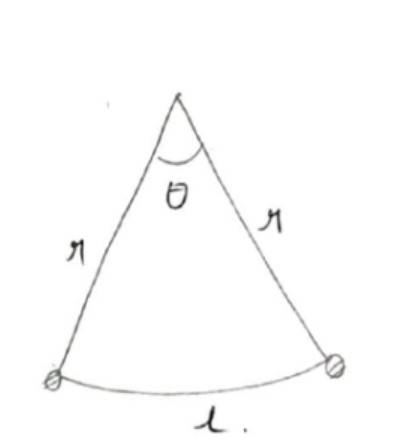
So, radius, r = cm = 20 cm
Length of chord (AB) = 20cm
In OAB
OA = OB=AB=20 cm
Hence, AOAB is equilateral triangle and end of the angle is 60°
:. Ø =60° = 60 *
radian = radian
Hence, length of minor are of the chord, l=rØ.
l = 20 * cm
l = cm.
New answer posted
7 months agoContributor-Level 10
4. Here l = 22cm.
r =100cm.
Ø =?
Hence by r =
= Ø = = radian
= * /π
= * 180° *
=
=12 = 12°
New answer posted
7 months ago3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Contributor-Level 10
3. Given that a wheel makes 360 revolutions in one minute
Then, number of revolutions in one second = =6.
In 1 complete revolution the wheel turns 360°= 2π radian.
So, In 6 revolution, the wheel will turns 6*2π radian = 12π radian.
Hence, in one second the wheel will turn an angle of 12π radian.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers