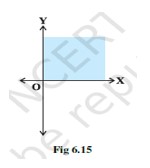
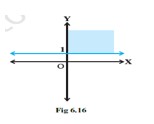
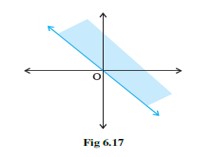
Linear Inequalities

  $x^2+y^2-2\sqrt[]{2}x-6\sqrt[]{2}y+14=0$

 centre $\left(\sqrt[]{2},3\sqrt[]{2}\right)$

radius  ${\left({\left(\sqrt[]{2}\right)}^2+{\left(3\sqrt[]{2}\right)}^2-14\right)}^{1/2}$

$={\left(2+18-14\right)}^{1/2}=\left(\sqrt[]{6}\right)$

${\left(x-2\sqrt[]{2}\right)}^2+{\left(y-2\sqrt[]{2}\right)}^2=r^2$

centre  $\left(2\sqrt[]{2},2\sqrt[]{2}\right)$

OA = $\sqrt[]{{\left(2\sqrt[]{2}-\sqrt[]{2}\right)}^2+{\left(2\sqrt[]{2}-3\sqrt[]{2}\right)}^2}=\sqrt[]{2+2}=2$                  

r² = ${\left(\sqrt[]{6}\right)}^2+{\left(2\right)}^2=6+4=10$  

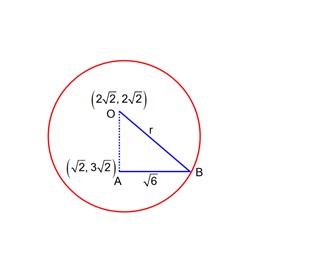
Let y = mx + c is the common tangent

$soc=\frac{1}{m}=\pm \frac{3}{2}\sqrt[]{1+m^2}\Rightarrow m^2=\frac{1}{3}$

so equation of common tangents will be

$y=\pm \frac{1}{\sqrt[]{3}}x\pm \sqrt[]{3}$

which intersects at Q (3, 0)

Major axis and minor axis of ellipse are 12 and 6. So eccentricity

$e^2=1-\frac{1}{4}=\frac{3}{4}$

and length of latus rectum

$=\frac{2b^2}{a}=3$

Hence

$\frac{\mathcal{l}}{e^2}=\frac{3}{3/4}=4$

$z^2+z+1=0\Rightarrow z=w,w^2$

$\left|{\displaystyle \sum _{n=1}^{15}{\left(z^n+{\left(-1\right)}^n\frac{1}{z^n}\right)}^2}\right|=\left|{\displaystyle \sum _{n=1}^{15}\left(z^{2n}+\frac{1}{z^{2n}}+2{\left(-1\right)}^n\right)}\right|=\left|{\displaystyle \sum _{n=1}^{15}{w}^{2n}+\frac{1}{w^{2n}}+2{\left(-1\right)}^n}\right|$

$=\left|\frac{w^2\left(1-1\right)}{1-w^2}+\frac{\frac{1}{w^2}\left(1-1\right)}{1-\frac{1}{w^2}}-2\right|=2$

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar

$\begin{array}{l}\left(i\right)-4x\ge 12\Rightarrow x\le -3\\ Hence,thefilleris\left(\le \right)\\ \left(ii\right)If-\frac{3}{4}x\le -3\Rightarrow x\ge 3x*\frac{4}{3}\Rightarrow x\ge 4\\ Hence,thefilleris\left(\ge \right)\\ \left(iii\right)If\frac{2}{x+2}>0\Rightarrow x>-2\\ Hence,thefilleris\left(>\right)\\ \left(iv\right)Ifx>-5\Rightarrow 4x>-20\\ Hence,thefilleris\left(>\right)\\ \left(v\right)Ifx>yandz<0,then\\ xz<yz\Rightarrow -xz>-yz\\ Hence,thefilleris\left(>\right)\\ \left(vi\right)Ifp>0andq<0,then\\ p-q>p\\ Hence,thefilleris\left(>\right)\\ \left(vii\right)If\left|x+2\right|>5then\\ x+2<-5orx+2>5\\ \Rightarrow x<-5-2orx>5-2\\ \Rightarrow x<-7orx>3\\ So,x\in \left(-\infty ,-7\right)\cup \left(3,\infty \right)\\ Hence,thefilleris\left(<\right)or\left(>\right)\\ \left(viii\right)If-2x+1\ge 9then\\ \Rightarrow -2x\ge 9-1\Rightarrow -2x\ge 8\Rightarrow 2x\le -8\Rightarrow x\le -4\\ Hence,thefilleris\left(\le \right)\end{array}$

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l}\left(i\right)Ifx<yandb<0\\ \Rightarrow \frac{x}{b}>\frac{y}{b}\\ Hence,statement\left(i\right)isFalse.\\ \left(ii\right)Ifx,y>0thenx>0,y>0orx<0,y<0\\ Hence,statement\left(ii\right)isFalse.\\ \left(iii\right)Ifxy>0thenx<0,andy<0\\ Hence,statement\left(iii\right)isTrue.\\ \left(iv\right)Ifxy<0thenx<0,y>0orx>0,y<0\\ Hence,statement\left(iv\right)isFalse.\\ \left(v\right)Ifx<-5andx<-2\Rightarrow x\in \left(-\infty ,-5\right)\\ Hence,statement\left(v\right)isTrue.\\ \left(vi\right)Ifx<-5andx>2thenxhasnovalue.\\ Hence,statement\left(vi\right)isFalse.\\ \left(vii\right)Ifx>-2andx<9\Rightarrow x\in \left(-2,9\right)\\ Hence,statement\left(vii\right)isTrue.\\ \left(viii\right)If\left|x\right|>5thenx<-5orx>5\\ \Rightarrow x\in \left(-\infty ,-5\right)\cup \left(5,\infty \right)\\ Hence,statement\left(viii\right)isFalse.\\ \left(ix\right)If\left|x\right|\le 4then-4\le x\le 4\\ \Rightarrow x\in \left[-4,4\right]\\ Hence,statement\left(ix\right)isTrue.\\ \left(x\right)Thegivengraphrepresentsx\le 3\\ Hence,statement\left(x\right)isFalse.\\ \left(xi\right)Thegivengraphrepresentsx\ge 0\\ Hence,statement\left(xi\right)isTrue.\\ \left(xii\right)Thegivengraphrepresentsy\ge 0\\ Hence,statement\left(xii\right)is\text{\&thins}\end{array}$

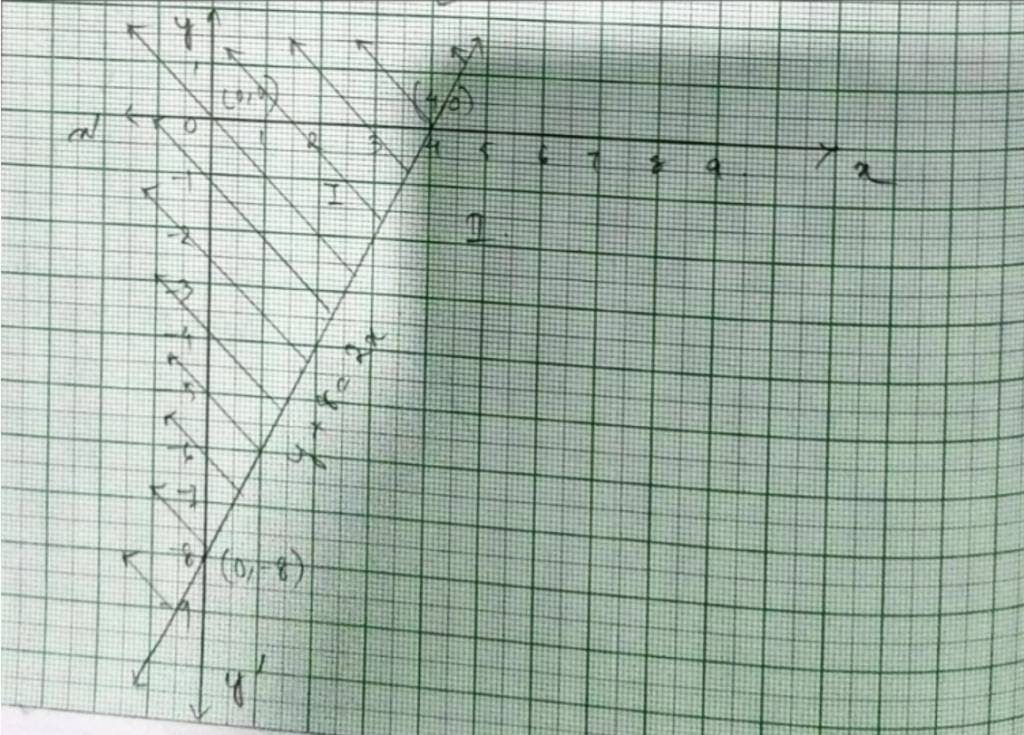
30. 

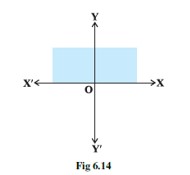
30. For inequality y+8 ≤ 2x, the equation of the line is y+8=2x. We consider the table below to plot of y+8=2x.

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ -8\end{array}|\begin{array}{l}4\\ 0\end{array}|$

The line devides the xy-plane into half planer I and II. We select a point (0,0) and check the correctness of the inequality.

i.e., 0+8 ≤ 2 * 0

0 ≤ 0 which is true.

So, the solution region is I which includes the rigin (0,0). The continuous line also indicates that any points on the line also satisfy the given inequality.

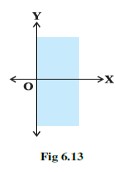
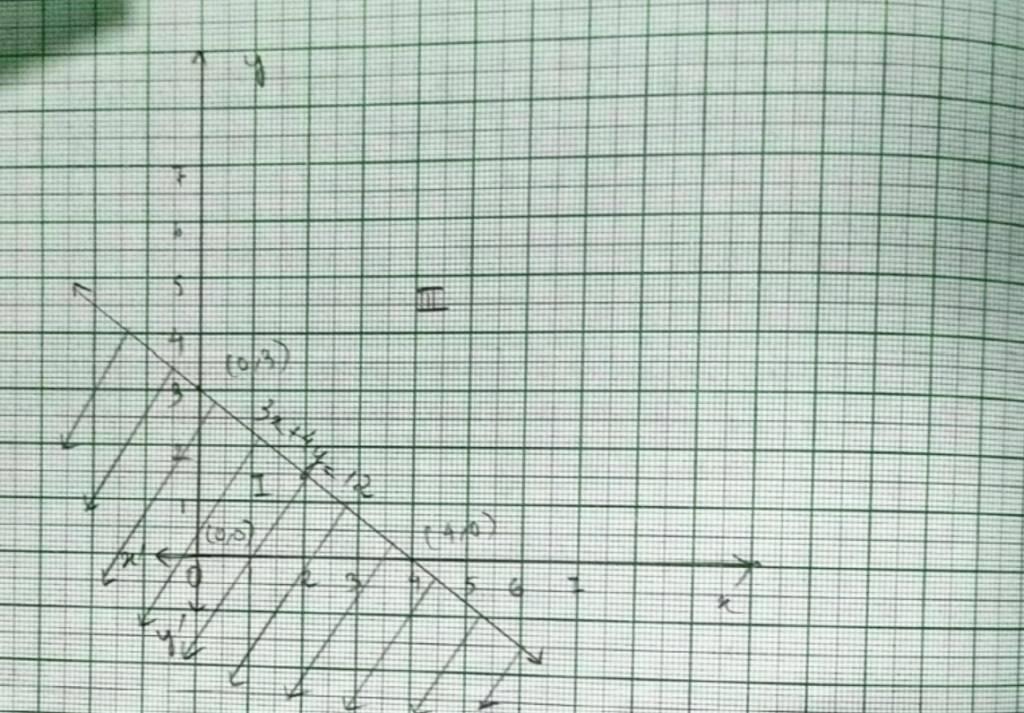
29. For inequality 3x+4y≥ 12 the equation of the line is 3x+4y=12

We consider the table below to plot 3x+4y=12.

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ 3\end{array}|\begin{array}{l}4\\ 0\end{array}|$

This line devides the xy-plane into half planer I and II.

We select point 0 (0,0) and check the correctness of the inequality.

i.e., 3 * 0+4 * 0 ≤ 12.

0+0 ≤ 12

0 ≤12 which is true.

So, the solution region is I which includes the origin (0,0). The continuous line also indicates that any points in the line also satisfy the given inequality.

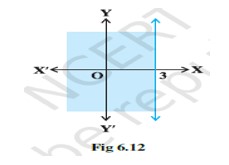
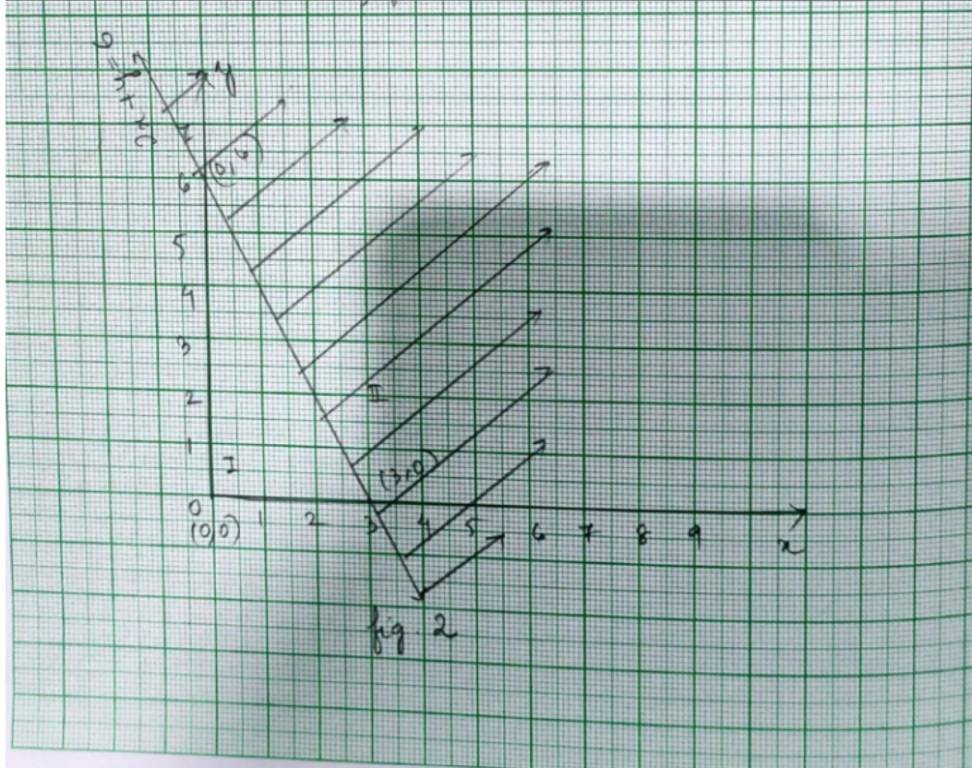
28. For inequality, 2x+y≥ 6, the equation of line is 2x+y=6.

We consider the table below to pot 2x+y=6.

$\begin{array}{l}x\\ y\end{array}|\begin{array}{l}0\\ 6\end{array}|\begin{array}{l}3\\ 0\end{array}|$

Graph of 2x+y=6 is given as a continuous line in fig 2.

This line divides xy-plane in two half planes I and II.

We select 0 (0,0) and check the correctness of the inequality.

is 2 * 0+0 ≥ 6.

0 ≥ 6 which is false.

So, the solution region is II where origin (0,0) is included.

The continuous line indicates that any point on the line. also satisfy the given inequality.