Class 12th
Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 9
Bandwidth
= (ω? + ω? ) - (ω? - ω? )
= 2ω?
= 2 (2πf? )
= 4πf?
= 2π (2f? )
= 2π (2*10? ) rad/s
= 2 * 10? Hz
= 200 kHz
New answer posted
4 months agoContributor-Level 10
T sin θ = (1/4πε? ) * q²/ (2lsinθ)²
T cos θ = mg
∴ tan θ = q² / (4πε? mg * 4l²sin²θ)
[tan θ ≈ θ, for small angle]
So, θ³ = q² / (16πε? mgl²)
θ = ( q² / (16πε? mgl²) )¹/³
Also separation = 2l sin θ ≈ 2lθ
= 2l ( q² / (16πε? mgl²) )¹/³
= ( 8q²l³ / (16πε? mgl²) )¹/³
= ( q²l / (2πε? mg) )¹/³
New answer posted
4 months agoContributor-Level 10
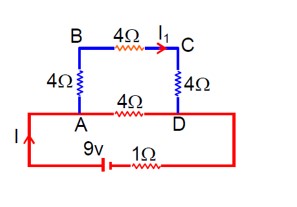
Each side of the square has a resistance of 16/4 = 4Ω.
The side AC has the 9V, 1Ω source.
The other three sides (AB, BD, DC) form a path with resistance 4+4+4 = 12Ω.
This is in parallel with the side AC (4Ω).
Total resistance of the loop part: (12*4)/ (12+4) = 48/16 = 3Ω.
Total resistance of the circuit: R_total = 3Ω + 1Ω (internal) = 4Ω.
Total current from source I = V/R_total = 9/4 A.
This current splits.
Current through path ABDC, I? = I * (R_AC / (R_ABDC + R_AC) = (9/4) * (4/16) = 9/16 A.
Potential at B: V_B = V_A - I? R_AB = 9 - (9/16)*4 = 9 - 9/4 = 27/4 V.
Potential at D: V_D = V_C + I? R_CD = 0 + (9/16)*4 = 9/4 V.
Potential drop a
New answer posted
4 months agoContributor-Level 10
Binding Energy = (Δm)c²
= [Zmp + (A-Z)mn - MAl]c²
= [ (13*1.00726 + 14*1.00866) - 27.18846] u
= [ (13.09438 + 14.12124) - 27.18846] u
= [27.21562 - 27.18846] u
= 0.02716 u
= 0.02716 x = 27.16x * 10? ³
New answer posted
4 months agoContributor-Level 10
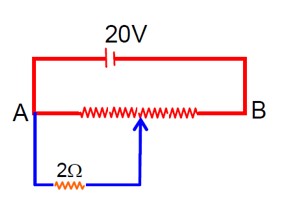
Applying nodal analysis at point X with potential xV:
(x-20)/5 + (x-0)/2 + (x-20)/5 = 0
2 (x-20) + 5x + 2 (x-20) = 0
9x - 80 = 0 => x = 80/9 V
Potential drop across 2Ω resistor = x = 80/9 V.
(Note: There seems to be a discrepancy in the provided solution and standard circuit analysis. The provided solution calculates the current junction, not a single point.)
The solution provided in the image calculates as:
(x-0)/5 + (x-20)/5 + (x-20)/2 = 0
2x + 2 (x-20) + 5 (x-20) = 0
9x - 140 = 0
=> x = 140/9 V
Potential drop across 2Ω = 20 - x = 20 - 140/9 = 40/9 V
New answer posted
4 months agoContributor-Level 10
By Einstein's equation of photoelectric effect,
hc/λ = hc/λ? + eVs
Now hc/λ = hc/λ? + e*4.8 . (i)
hc/ (2λ) = hc/λ? + e*1.6 . (ii)
Multiply (ii) by 2:
hc/λ = 2hc/λ? + e*3.2 . (iii)
Equating (i) and (iii):
hc/λ? + 4.8e = 2hc/λ? + 3.2e
1.6e = hc/λ?
Substitute this into (i)
hc/λ = 1.6e + 4.8e = 6.4e
Substitute this into (ii)
(6.4e)/2 = hc/λ? + 1.6e
3.2e = hc/λ? + 1.6e
1.6e = hc/λ?
From (i): hc/λ = hc/λ? + 3 (hc/λ? ) = 4hc/λ?
λ? = 4λ
New answer posted
4 months agoContributor-Level 9
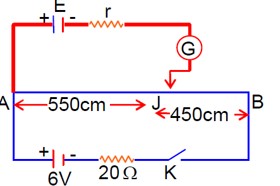
Maximum value of emf is measured when pointer is at B with I? = 0.
So, I_AB = 6 / (20 + 0.1 * 1000) = 6/120 = 1/20 A
V_AB = E = I_AB * R_AB
= (1/20) * 100
= 5V
New answer posted
4 months agoContributor-Level 9
Reflected wave will be 3.1cos [1.8z + (5.4*10? )t] î N/C
K = 2π/λ
⇒ 1.8 = 2π/λ
λ = 2π/1.8 = π/0.9 = 10π/9 = (10/9) * 3.14
= 3.48m
New answer posted
4 months agoContributor-Level 10
Enet = Eo/k
Enet = E_free - E_bound = qf/Aε? - qb/Aε?
Eo = qf/Aε?
So, (qf-qb)/Aε? = qf/ (kAε? )
qf - qb = qf/k
qb = qf (1 - 1/k)
New answer posted
4 months agoContributor-Level 10
Given 2q? = q? and v? /v? = 2/3, m? = m?
r = mv/qB
r? /r? = (m? /m? ) * (v? /v? ) * (q? /q? )
r? /r? = (1) * (2/3) * (2) = 4/3
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers