Complex Numbers and Quadratic Equations
Get insights from 193 questions on Complex Numbers and Quadratic Equations, answered by students, alumni, and experts. You may also ask and answer any question you like about Complex Numbers and Quadratic Equations
- 193
Questions
- 0
Discussions
- 0
Active Users
- 0
Followers
Have a question about Complex Numbers and Quadratic Equations? Ask our experts
Keep it short & simple. Type complete word. Avoid abusive language.
A ray of light coming from the point (2,2√3) is incident at an angle 30° on the line x=1 at the point A. The ray gets reflected on the line x=1 and meets x-axis at the point B. Then, the line AB passes through the point:
A ray of light coming from the point (2,2√3) is incident at an angle 30° on the line x=1 at the point A. The ray gets reflected on the line x=1 and meets x-axis at the point B. Then, the line AB passes through the point:
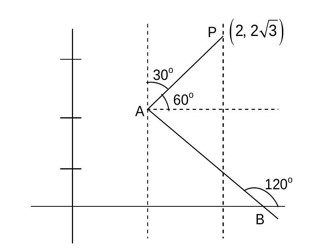
m (AP)=tan60°=√3. y-2√3=√3 (x-2). At x=1, y=√3. A= (1, √3).
m (AB)=tan120°=-√3. y-√3=-√3 (x-1) ⇒ √3x+y=2√3. (3, -√3) satisfies
Upvote 
Let z = (3+isinθ)/(4-icosθ) x (4+icosθ)/(4+icosθ)
= (12 - sinθcosθ + i(4sinθ + 3cosθ))/(16 + cos²θ)
z is real
∴ 4sinθ + 3cosθ = 0
⇒ tanθ = -3/4 [? θ lies is 2nd quadrant]
arg(sinθ + icosθ) = π + tan?¹(cosθ/sinθ)
= π - tan?¹(4/3)
Upvote Let and be the roots of the equation . If , then which one of the following statements is not true?
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Let and be the roots of the equation . If , then which one of the following statements is not true?
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
p? = α? + β?
= (α + 1)² . α + (β - 1)² . β
= 5α + 5β + 6
= 5(1) + 6 = 11
p? = α² + β² = α + β + 2 = 3
p? = α³ + β³ = (α + 1) . α + (β + 1) . β
= 1 + 3 = 4
Hence p? ≠ p? . p?
Upvote If α and β are the roots of the equation, 7x²-3x-2=0, then the value of α/(1-α²) + β/(1-β²) is equal to:
If α and β are the roots of the equation, 7x²-3x-2=0, then the value of α/(1-α²) + β/(1-β²) is equal to:
α+β = 3/7, αβ = -2/7
α/ (1-α²) + β/ (1-β²) = (α+β) - αβ (α+β) / (1-α²) (1-β²)
= (α+β) - αβ (α+β) / (1 + (αβ)² - (α+β)² - 2αβ)
= (3/7) + (2/7) (3/7) / (1 + (-2/7)² - (3/7)² - 2 (-2/7) = 27/16
Upvote (-1+i√3)/ (1-i)³? = (2 (cos (2π/3) + isin (2π/3)/ (√2 (cos (-π/4) - isin (-π/4)³?
= (2³? (cos20π + isin20π)/ (2¹? (cos (-15π/2) - isin (-15π/2)
= (2¹? (1 + 0i)/ (0 + i) = -2¹? i
Upvote The equation of a circle is Re(z²) + 2(Im(z))² + 2Re(z) = 0, where z = x + iy. A line which passes through the center of the given circle and the vertex of the parabola, x² - 6x - y + 13 = 0, has y-intercept equal to……….
The equation of a circle is Re(z²) + 2(Im(z))² + 2Re(z) = 0, where z = x + iy. A line which passes through the center of the given circle and the vertex of the parabola, x² - 6x - y + 13 = 0, has y-intercept equal to……….
Re (z²) = x²-y². 2 (Im (z)² = 2y². 2Re (z) = 2x.
x²-y²+2y²+2x=0 ⇒ x²+y²+2x=0.
(x+1)²+y²=1. Center (-1,0).
Parabola: x²-6x+9 = y-13+9 ⇒ (x-3)²=y-4. Vertex (3,4).
Line through (-1,0) and (3,4): slope = (4-0)/ (3- (-1) = 1.
y-0 = 1 (x+1) ⇒ y=x+1.
y-intercept is 1.
Upvote Let α, β be two roots of the equation x² + (20)¹/⁴x + (5)¹/² = 0 Then α⁸ + β⁸ is equal to:
Let α, β be two roots of the equation x² + (20)¹/⁴x + (5)¹/² = 0 Then α⁸ + β⁸ is equal to:
x? + 2 (20)¹/? x³ + (20)¹/²x² + . No.
x² = - (20)¹/? x - (5)¹/².
α+β = - (20)¹/? , αβ=5¹/².
α²+β² = (α+β)²-2αβ = (20)¹/² - 2 (5)¹/² = 0.
α? +β? = (α²+β²)² - 2 (αβ)² = 0 - 2 (5) = -10.
α? +β? = (α? +β? )² - 2 (αβ)? = (-10)² - 2 (5)² = 100 - 50 = 50.
Upvote Let C be the set of all complex numbers. Let
S₁ = {z ∈ C | |z - 3 - 2i|² = 8},
S₂ = {z ∈ C | Re(z) ≥ 5} and
S₃ = {z ∈ C | |z - z̄| ≥ 8}.
Then the number of element in S₁ ∩ S₂ ∩ S₃ is equal to:
Let C be the set of all complex numbers. Let
S₁ = {z ∈ C | |z - 3 - 2i|² = 8},
S₂ = {z ∈ C | Re(z) ≥ 5} and
S₃ = {z ∈ C | |z - z̄| ≥ 8}.
Then the number of element in S₁ ∩ S₂ ∩ S₃ is equal to:
S? : |z - 3 - 2i|² = 8
|z - (3 + 2i)| = 2√2
(x - 3)² + (y - 2)² = (2√2)²
S? : Re (z) ≥ 5
x ≥ 5
S? : |z - z? | ≥ 8
|2iy| ≥ 8
2|y| ≥ 8
|y| ≥ 4
y ≥ 4 or y ≤ -4
From the graph of the circle (S? ) and the regions (S? and S? ), we can see that there is one point of intersection at (5, 4).
∴ n (S? ∩ S? ∩ S? ) = 1
Upvote The number of real solutions of the equation, x² - |x| - 12 = 0 is:
The number of real solutions of the equation, x² - |x| - 12 = 0 is:
x² - |x| - 12 = 0
Case 1: x ≥ 0, |x| = x
x² - x - 12 = 0
(x-4) (x+3) = 0, x=4 (x=-3 is rejected)
Case 2: x < 0, |x| = -x
x² + x - 12 = 0
(x+4) (x-3) = 0, x=-4 (x=3 is rejected)
Two real solutions: 4 and -4.
Upvote Let z be those complex numbers which satisfy
If the maximum value of <!-- [if gte mso 9]><xml>
Let z be those complex numbers which satisfy
If the maximum value of <!-- [if gte mso 9]><xml>
->Represent a circle
->Represent a line X – y
So max |z + 1|2 = AQ2
Hence α + β) = 48
Upvote