Definite Integrals

I = ∫? ² (x³+|x|)/ (e|x|+1) dx . (i)
I = ∫? ² (x³+|x|)/ (e? |x|+1) dx . (ii)
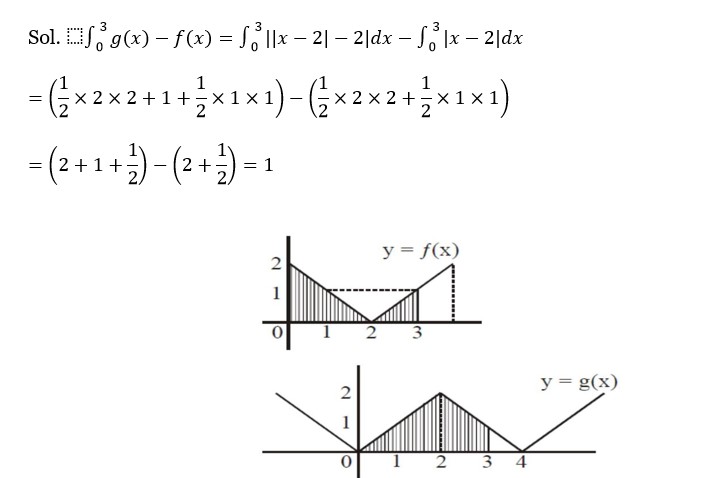
= ∫? ² |x| dx = 2∫? ² x dx
= [x²/2]? ² = (16/4 + 4/2) - 0
= 4+2=6

f (x) + f (x + 1) = 2 (1)
replace x with x + 1: f (x + 1) + f (x + 2) = 2 (2)
(2) - (1) ⇒ f (x + 2) = f (x)
∴ f (x) is periodic with period 2.
I? = ∫? f (x)dx = 4 ∫? ² f (x)dx.
I? = ∫? ³ f (x)dx = ∫? f (u-1)du. Let u = x+1.
I? = ∫? f (x-1)dx = 2 ∫? ² f (x-1)dx.
From (1), f (x-1) + f (x) = 2.
I? + 2I? = 4∫? ² f (x)dx + 2 (2∫? ² f (x-1)dx) = 4∫? ² f (x)dx + 4∫? ² (2 - f (x)dx
= 4∫? ² (f (x) + 2 - f (x)dx = 4∫? ² 2 dx = 4 [2x] from 0 to 2 = 16.

Answer given by NTS is (1) which is wrong.
I = 1/ (a+b) ∫? x [f (x) + f (x+1)]dx . (1)
Using the property x → a + b - x
I = 1/ (a+b) ∫? (a+b-x) [f (a+b-x) + f (a+b+1-x)]dx
Given f (a+b+1-x) = f (x)
I = 1/ (a+b) ∫? (a+b-x) [f (x+1) + f (x)]dx . (2)
Adding (1) and (2):
2I = 1/ (a+b) ∫? (a+b) [f (x) + f (x+1)]dx
2I = ∫? [f (x) + f (x+1)]dx
2I = ∫? f (x)dx + ∫? f (x+1)dx
Let x+1 = t in the second integral, so dx = dt.
When x=a, t=a+1. When x=b, t=b+1.
∫? f (x+1)dx = ∫? ¹ f (t)dt = ∫? ¹ f (x)dx

P (x) = x² + bx + c.
Given ∫? ¹ P (x) dx = 1.
∫? ¹ (x² + bx + c) dx = [x³/3 + bx²/2 + cx] from 0 to 1 = 1/3 + b/2 + c = 1.
2 + 3b + 6c = 6 => 3b + 6c = 4 - (i)
When P (x) is divided by (x-2), the remainder is 5. So, P (2) = 5.
(2)² + b (2) + c = 5 => 4 + 2b + c = 5 => 2b + c = 1 - (ii)
From (ii), c = 1 - 2b. Substitute into (i):
3b + 6 (1 - 2b) = 4
3b + 6 - 12b = 4
-9b = -2 => b = 2/9.
c = 1 - 2 (2/9) = 1 - 4/9 = 5/9.
We need to find 9 (b+c).
9 (2/9 + 5/9) = 9 (7/9) = 7.

Find the number of solutions for 2tan(x) = π/2 - x in [0, 2π].
This is equivalent to finding the number of intersection points of the graphs y = tan(x) and y = (π/4) - x/2.
Let's sketch the graphs:

y = tan(x) has vertical asymptotes at x = π/2, 3π/2.

y = (π/4) - x/2 is a straight line with a negative slope.
At x=0, y=π/4.
At x=π/2, y=0.
At x=π, y=-π/4.
At x=2π, y=-3π/4.
By observing the graphs, there will be one intersection in (0, π/2), one in (π/2, 3π/2), and one in (3π/2, 2π].
Total number of solutions is 3.

The equation of a plane parallel to x - 2y + 2z - 3 = 0 is x - 2y + 2z + λ = 0.
The distance from the point (1, 2, 3) to this plane is 1.
|1 - 2 (2) + 2 (3) + λ| / √ (1² + (-2)² + 2²) = 1
|1 - 4 + 6 + λ| / √9 = 1
|3 + λ| / 3 = 1
|3 + λ| = 3
3 + λ = 3 or 3 + λ = -3
λ = 0 or λ = -6.

I = ∫ from -π/2 to π/2 (1 / (1+e^ (sin x) dx
I = ∫ from -π/2 to π/2 (e^ (sin x) / (1+e^ (sin x) dx
2I = ∫ from -π/2 to π/2 1dx ⇒ I = 1/2 ∫ from -π/2 to π/2 dx
I = 1/2 [x] from -π/2 to π/2 ⇒ I = π/2

 f (x) = ∫ (from 1 to 3) (√x dx)/ (1+x)² = ∫ (from 1 to √3) (t⋅2tdt)/ (1+t²)² (put √x = t)
= [ (-t/ (1+t²)] (from 1 to √3) + [tan? ¹t] (from 1 to √3) [Applying by parts]
= (-√3/4 + 1/2) + (π/3 - π/4)
= (-√3+2)/4 + π/12