Linear Inequalities

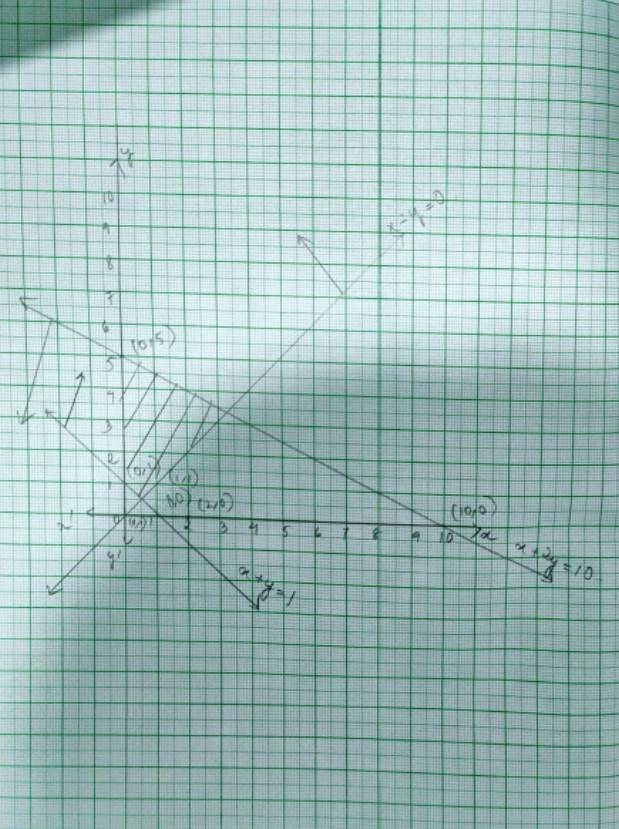
51. The given system of inequality is

x+2y≤ 10- (1)

x+y≥ 1 - (2)

x – y ≤ 0 - (3)

x≥ 0 and y≥ 0 - (4)

The corresponding equation of (1), (2) and (3) are

x + 2y = 10

and x + y =1

and x – y = 0

Putting (2,0)= (x, y) in inequality (1), (2) and (3),

2+2 * 0 ≤ 10 =>  2≤ 10 is true.

and 2+0 ≥ 1 =>  2 ≥ 1 is true.

and 2 – 0 ≤ 0  => 2 ≤ 0 is false.

So, the solution of inequality (1) and (2) is the plane that includes point (2,0) whereas the solution of inequality (3) is the plane which includes point (2, 0)

∴ The shaded region represents the solution of the given system of inequality.

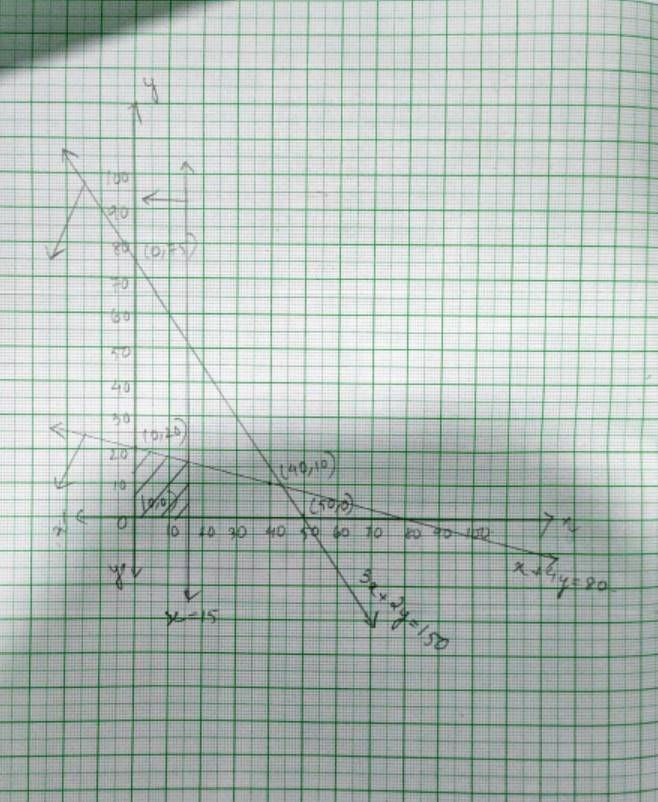
50.The given system of inequality is

3x+2y≤ 150- (1)

x+4y≤ 80- (2)

x≤ 15 - (3)

y≥ 0 and x≥ 0 - (4)

The corresponding equation of (1) and (2) are

3x + 2y = 150

and x + 4y =80

Putting (0,0)= (x, y) in inequality (1) and (2) we get,

3 * 0+2 * 0 ≤ 150  => 0 ≤ 150 is true.

and 0+4 * 0 ≤ 80  => 0 ≤ 80 is true.

So, the solution plane of both inequality (1) and (2) includes the origin (0,0).

∴ The shaded region is the solution of the given system of inequality.

49. The given system of inequality is

4x+3y≤ 60- (1)

y≥ 2x- (2)

x≥ 3- (3)

andx, y ≥ 0- (4)

The corresponding equation of inequality (1) and (2) are

4x+3y= 60

and y = 2x

Putting (1,0) in inequality (1) and (2) we get,

4 * 1+3 * 0 ≤ 60

4 ≤ 60 which is true.

and 0 ≥ 2 * 1

0 ≥ 2 which is false.

So, solution of inequality (1) includes the plane with point (1,0) whereas the solution of inequality (2) excludes the plane with point (1,0).

? The shaded region is the solution of the given system of inequality.

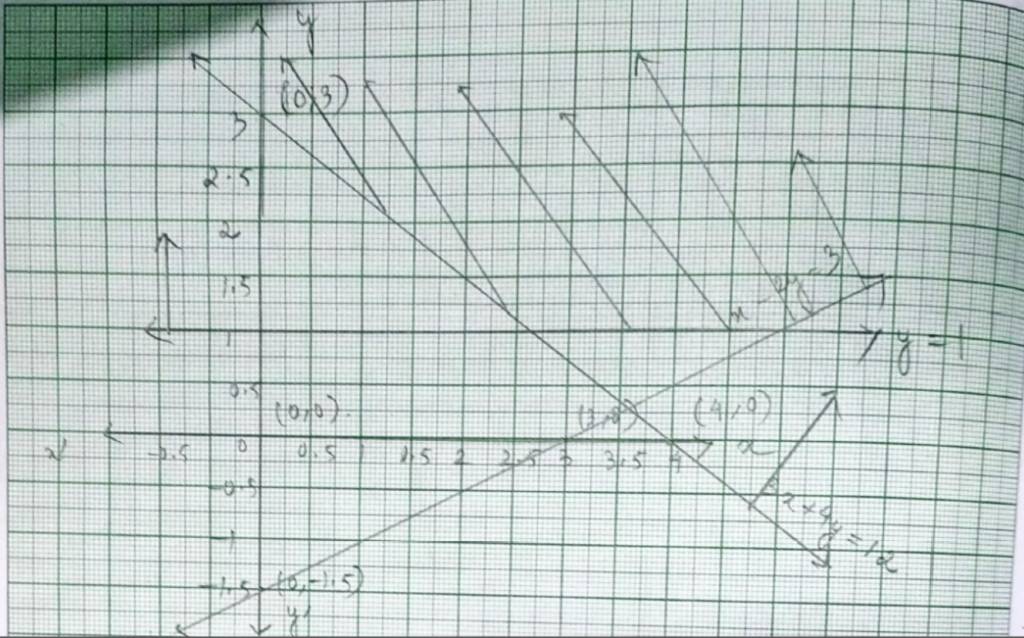
48. The given system of inequality is

x – 2y≤ 3 - (1)

3x – 4y≥12- (2)

x ≥ 0 - (3)

y≥ 1 - (4)

The corresponding equation of (1) and (2) are

x – 2y= 3

and 3x – 4y=12

Putting (x, y)= (0,0) in inequality (1) and (2),

0 – 2 * 0 ≤ 3   => 0 ≤ 3 is true.

and 3 * 0+4 * 0 ≥ 12   => 0 ≥ 12 is false.

So, solution of inequality (1) includes plane wilt origin (0,0) while solution plane of inequality (2) includes the origin.

∴ The shaded portion determines the solution region of the given system of inequality.

47. The given system of inequality is

2x + y ≥ 4- (1)

x + y ≤ 3- (2)

2x – 3y ≤ 6- (3)

The corresponding equation are

2x + y = 4

and x + y = 3

and 2x + 3y = 6

Putting (x, y)= (0,0) in (1), (2) and (3),

2 * 0+0 ≥ 4

0 ≥ 4 which is false.

and 0+0 ≤ 3   => 0 ≤ 3 which is true.

and 2 * 0 – 3 * 0 ≤ 6  => 0 ≤ 6which is also true.

So, solution of inequality (1) excludes plane with origin while solution of inequality (2) and (3) includes the plane with origin.

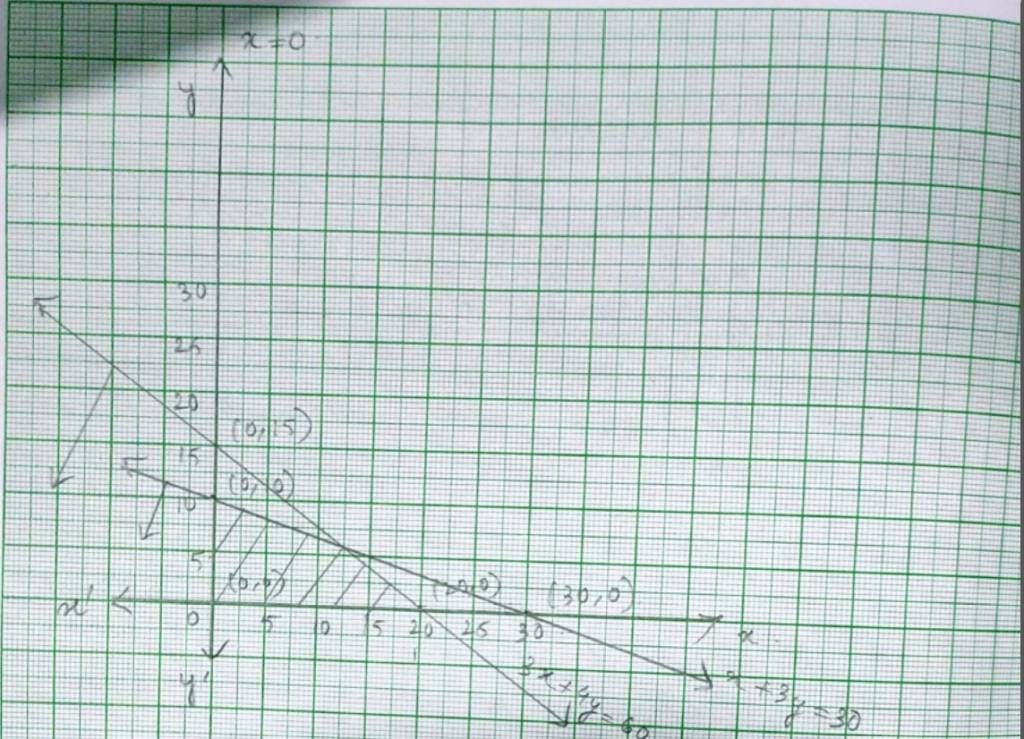
46. The given system of inequality is

3x+4y ≤ 60 - (1)

x+3y ≤ 30- (2)

x≥ 0 - (3)

xy≥ 0 - (4)

The corresponding equation of (1) and (2) are

3x + 4y = 60

and x + 3y = 30

Putting (x, y)= (0,0) in equality (1) and (2),

3 * 0+4 * 0 ≤ 60 and 0+3 * 0 ≤ 30

0 ≤ 60 which is true and 0 ≤ 30 which is true

So, the solution plane of inequality (1) and (2) is the plane including origin (0,0)

∴ The shaded portion is the solution of the given system of inequality.

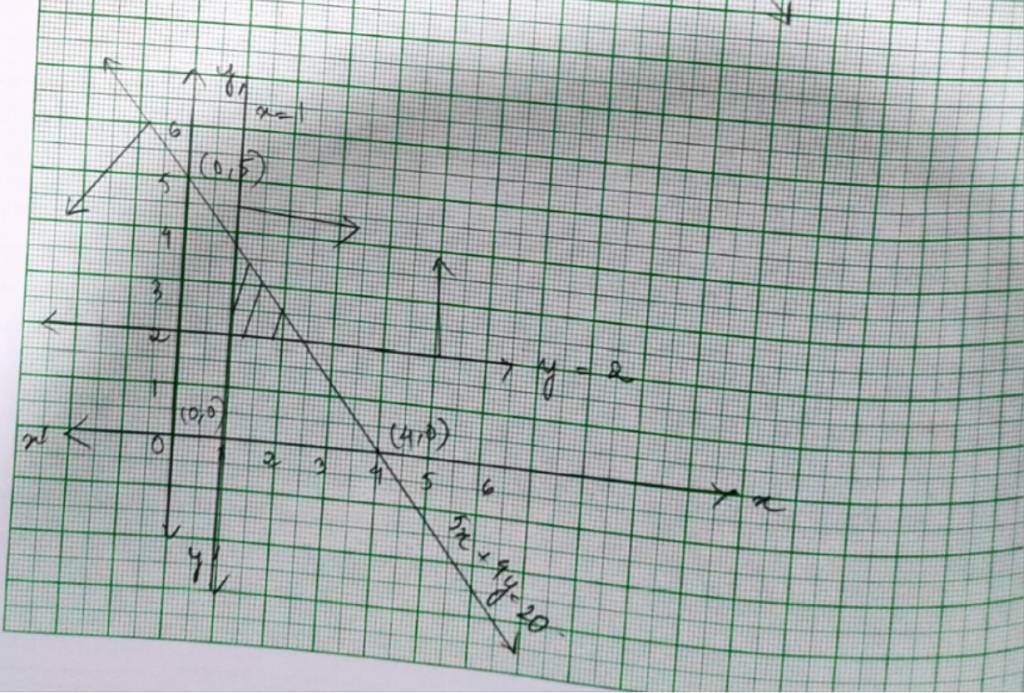
45. The given system of inequality is

5x+4y≤ 20 - (1)

x≥ 1 - (2)

and  y≥ 2 - (3)

The equation of inequality (1) is 5x+4y=20.

Putting (x, y)= (0,0) in inequality (1) we get,

5 * 0+4 * 0 ≤ 20   => 0 ≤ 20 which is true.

So, the solution region of inequality (1) includes the plane with origin (0,0).

∴ The shaded region indicates the solution of the given system of inequality.

44. The given system of inequality is

x+y≤ 9- (1)

y>x- (2)

x≥ 0 - (3)

The corresponding equation of (1) is x+y=9 and (2) is y=x

Substituting (x, y)= (0,0) in (1),

0+0 ≤ 9  => 0 ≤ 9 which is true.

And putting (1,0) in (2)

0> 1which is false.

So, solution region of inequality (1) includes origin (0,0) and solution region of inequality (2) excludes plane having (1,0).

? Solution of region of given system of inequality is the shaded region.

43. Given system of inequality is

2x+y≥ 8- (1)

x+2y≥ 10- (2)

The corresponding equations are

2x + y = 8

and x + 2y = 10

Now, putting (x, y)= (0,0) in inequality (1) and (2),

2 * 0+8 ≥ 8

0 ≥ 8 which is not true.

and 0+2 * 0 ≥ 10

0 ≥ 10 which is not true.

So, solution of plane of inequality (1) and (2) does not include the origin (0,0)

? The required solution of the given system of inequality is the shaded region.