Linear Inequalities
Get insights from 69 questions on Linear Inequalities, answered by students, alumni, and experts. You may also ask and answer any question you like about Linear Inequalities
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
32. For the inequality, 2x – 3y>6 the eqn is 2x – 3y=6. We consider the table below to plot 2x – 3y=6.
This line divides the xy-plane into half planer I and II. We select point (0,0) and check the correctness of the inequality.
2 * 0 – 3 * 0>6
0>6 which is false.
So, the solution region is II which does not includes the origin (0,0).
The dotted line indicates that the any point on the line does not satisfy the given inequality.
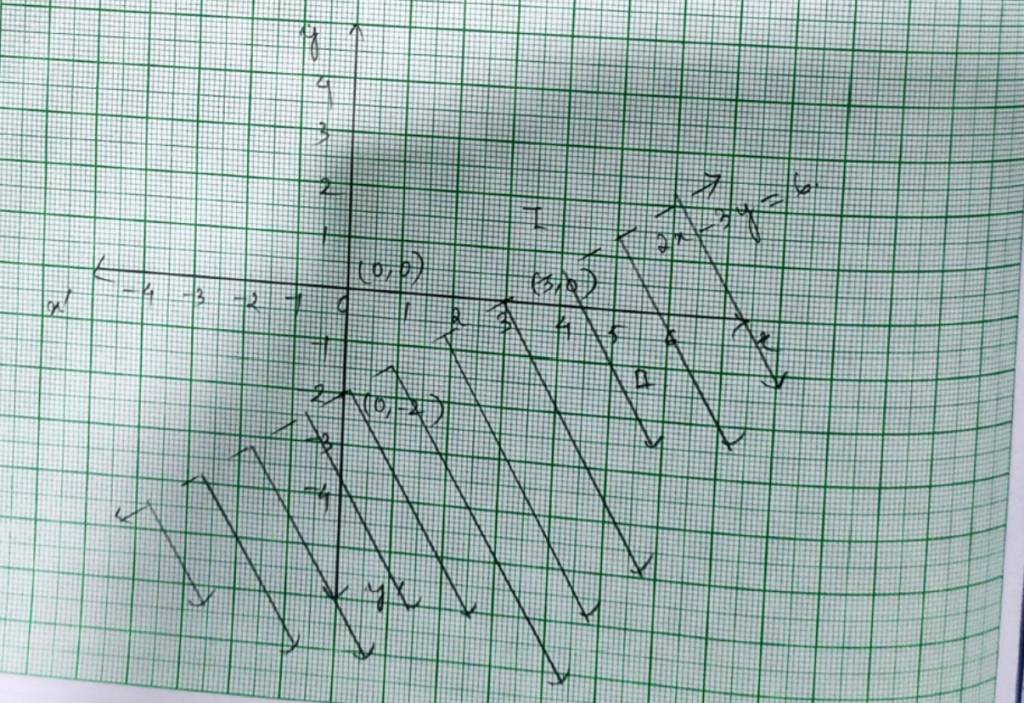
New answer posted
7 months agoContributor-Level 10
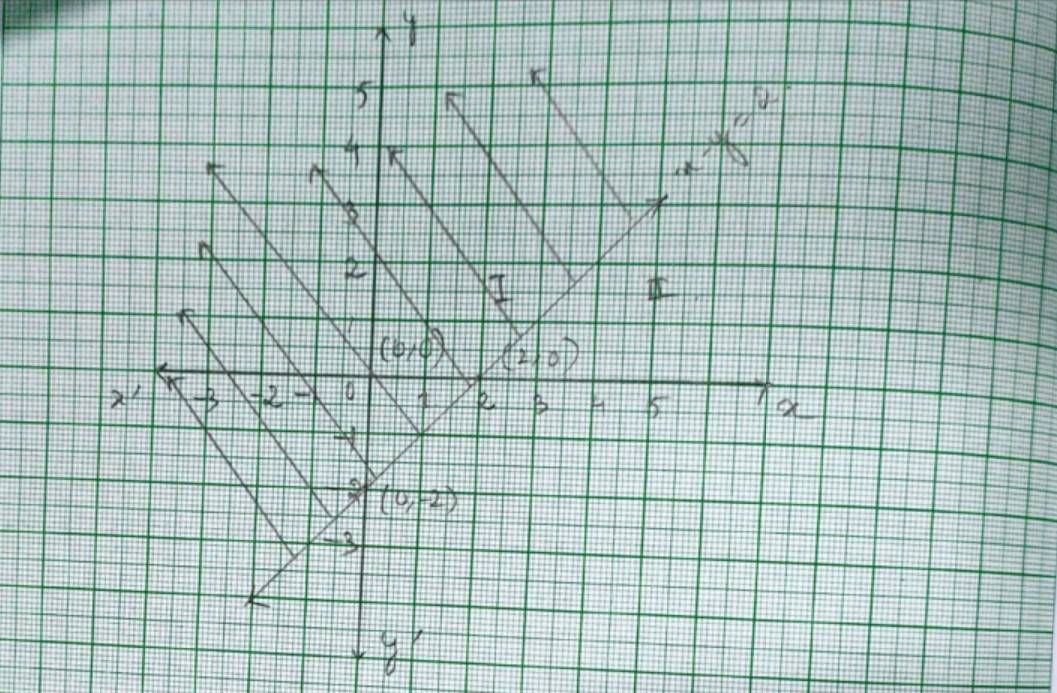
31. For the inequality x – y≤ 2 so the equation of line is x – y=2. We consider the table below to plat x – y=2
This line divides the xy-plane into half planer I and II. We select point (0,0) and check the correctness of the inequality.
0 – 0 ≤ 2
0 ≤ 2 which is true.
So, the solution region is I which includes the origin (0,0). The continuous line also indicates that any point on the line also satisfy the given inequality.
New answer posted
7 months agoContributor-Level 10
27. For inequality, x+y < 5, the equation of line is x+y = 5.
We consider the tableto plot x+y=5.
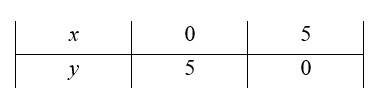
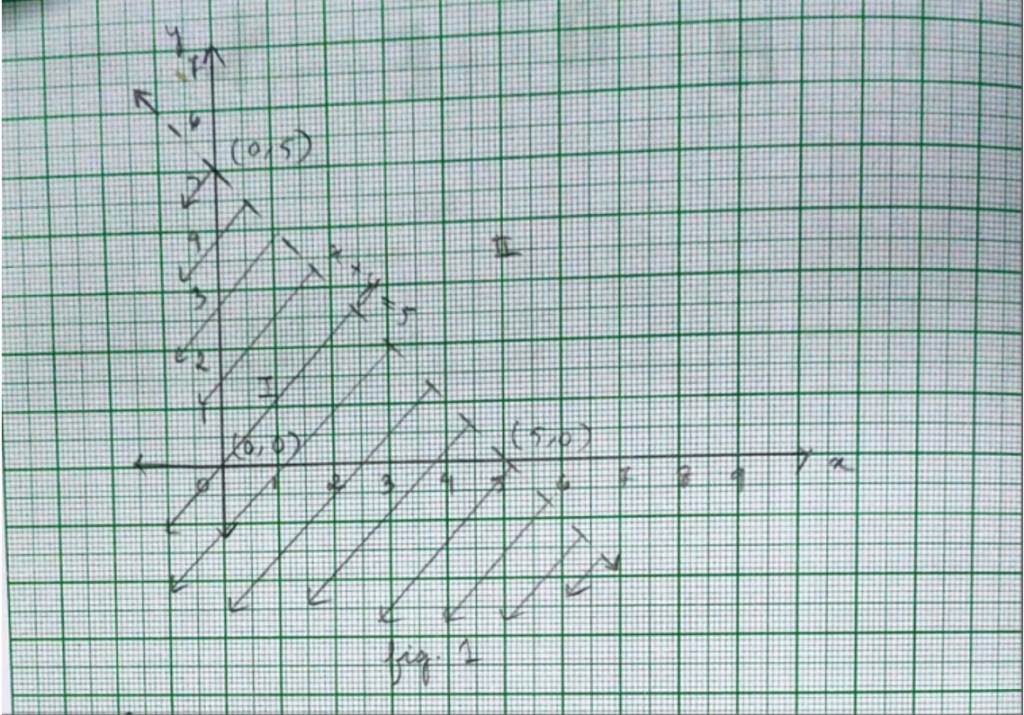
Graph of x+y = 5 is given as dotted line in fig 1. This lines divides by plane in two half planes I and II. We select a point not on the line, say (0,0) which lies in region I.
Since, 0+0 < 5
0 < 5 is true.
The solution region is I. (where origin (0,0) is included)
The dotted line indicates that any point on the line does not satisfy the given inequality.
New answer posted
7 months agoContributor-Level 10
26. Let 'x' cm be the length of the shortest piece.
Then, the two other remaining length is.
(x + 3) cm and (2x). cm.
So, given that,
2x - (x + 3) ≥ 5 cm.
2x- x - 3 ≥ 5.
x ≥ 5 + 3
x ≥ 8.
And. total length ≤ 91 cm
x + (x + 3) + 2x ≤ 91
4x + 3 ≤ 91
4x + 3 ≤ 91 - 3
x ≤ 22.
? 8 ≤ x ≤ 22.
Hence the length of the shortest board is greater than or equal to 8 cm and less than or equal to 22 cm.
New answer posted
7 months agoContributor-Level 10
25. Let x cm be the shortest side of the triangle.
Thus, the other 2 sides are “3x” cm and “3x - 2” cm
Given, perimeter of A triangle ≥ 61
x + 3x - 3x- 2 ≥ 61
7x - 21 ≥ 61
7x ≥ 61 + 21
x ≥ 9.
The minimum length of the shortest side is 9 cm.
New answer posted
7 months agoContributor-Level 10
24. Let x be the smaller no. of the two consecutive even positive integers, hence the other number is x + 2. (Two consecutive even no. differs by 2).
Then, x > 5, x + 2 > 5 => a> 3.
And x + (x + 2) < 23
2x + 2 < 23
2x < 23 - 2
2x < 21
So, 5 < x
Hence, x can take the value 6, 8 and 10.
So, the required possible pair is given by (x, x + 2) are (6, 8), (8, 10) and (10, 12).
New answer posted
7 months agoContributor-Level 10
23. Let x be the smaller of the consecutive odd positive integers, then the. other is x + 2 {Since the consecutive odd number are differ by 2.}
then the. other is x + 2
so, x < 10 and x + 2 < 10 x< 8
and x + (x + 2) > 11.
2x > 11 - 2
2x > 9
and hence,
4.5 As x ∈ z, x = 5 and x = 7 and x is odd The reqd. possible pairs by (x, x + 2) are (5, 7), (7, 9).
New answer posted
7 months agoContributor-Level 10
22. Let 'x' be the marks obtained by Sunita in the 5th exam.
Then, average marks ≥ 90.
.
368 + x ≥ 90 * 5.
368 + x ≥ 450.
x ≥ 450 - 368.
x ≥ 82.
Minimum mark required= 82.
New answer posted
7 months agoContributor-Level 10
21. Let x be the marks obtained by Ravi in third test.
Then, average mark ≥ 60
145 + x ≥ 180.
x ≥180 - 145
x ≥ 35.
So minimum mark required = 35.
New answer posted
7 months agoContributor-Level 10
20. Given,
15x ≥ 2 [25x –10 –21x + 9].
15x ≥ 2 [4x –1]
15x ≥ 8x –2
15x – 8x ≥ –2
7x ≥ –2
x ≥
So, x
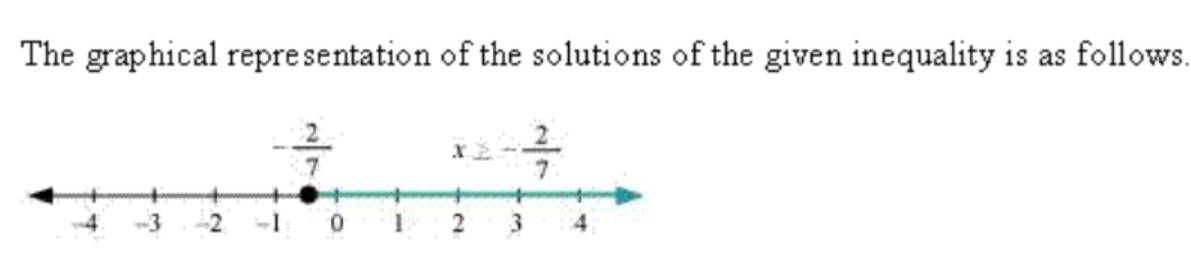
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
