Photoelectric Effect
Get insights from 18 questions on Photoelectric Effect, answered by students, alumni, and experts. You may also ask and answer any question you like about Photoelectric Effect
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 10
hc/λ = K? + φ [given φ is negligible]
So, hc/λ = K?
λ? = h/√ (2mK? ²) ⇒ K? = h²/ (2mλ? ²)
(hc)/λ = h²/ (2mλ? ²) ⇒ λ = (2mc/h)λ? ²
New answer posted
3 months agoContributor-Level 10
The equation representing the photoelectric effect is given as:
(1/2)mv? ² = hf? - φ . (1)
This continues the solution from number 6 on the previous page.
(1/2)mv? ² = hf? - φ . (2)
With the help of equations (1) and (2), we can write:
v? ² - v? ² = (2h/m) (f? - f? )
New answer posted
3 months agoContributor-Level 10
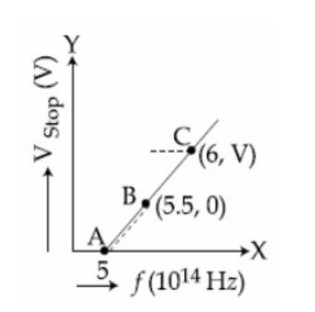
eVs = hv – φ
At Vs = 0 ⇒ hv = φ
⇒ φ = [6.62 * 10?³?][10¹?][5.5]
⇒ φ = ([6.62 * 10?³?][10¹?][5.5]eV) / [1.6 * 10?¹?]
= 2.27
New answer posted
3 months agoContributor-Level 10
If the work function of the metal is φ, then the kinetic energy (K.E.) of the emitted photoelectron is given by Einstein's photoelectric equation:
K.E. = hν - φ = (hc/λ) - φ
Case 1: λ? = 500 nm
K? = (hc/λ? ) - φ
Case 2: λ? = 200 nm
K? = (hc/λ? ) - φ
Given, K? = 3K?
So, (hc/λ? ) - φ = 3 * [ (hc/λ? ) - φ]
(hc/λ? ) - φ = 3 (hc/λ? ) - 3φ
2φ = 3 (hc/λ? ) - (hc/λ? )
2φ = hc * (3/λ? - 1/λ? )
φ = (hc/2) * [3/ (500 nm) - 1/ (200 nm)]
φ = (hc/2) * [ (6 - 5) / 1000 nm]
φ = hc / 2000 nm
Using hc ≈ 1240 eV·nm
φ = 1240 eV·nm / 2000 nm = 0.62 eV
New answer posted
3 months agoContributor-Level 10
E? = φ + K?
E? = φ + K?
E? - E? = K? - K?
Now V? /V? = 2
K? /K? = 4; K? = 4K?
Now from equation (2)
⇒ 4 - 2.5 = 4K? - K?
1.5 = 3K?
K? = 0.5eV
Now putting this
Value in equation (2)
2.5 = φ + 0.5eV
φ = 2eV
New answer posted
4 months agoContributor-Level 10
Stopping potential defined in terms of wavelength as :
Using above two equation we can calculate :
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 680k Reviews
- 1800k Answers