Physics NCERT Exemplar Solutions Class 11th Chapter Four

This is a Long Answer Type Question as classified in NCERT Exemplar

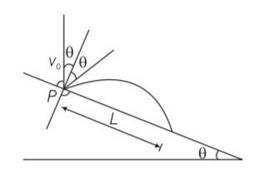
Explanation – particle is projected from the point O.

Let time taken in reaching from point O to point P is T.

for journey O to P

y=0,u_y= V_osin $\beta$ ,a_y= -gcos $\alpha ,t=T$

y=u_yt + $\frac{1}{2}{a}_y{t}^2$

0= V_osin $\beta T+\frac{1}{2}\left(-gcos\alpha \right)T^2$

T[V_osin $\beta -\frac{gcos\alpha }{2}$ T]=0

T = time of flight = $\frac{2V_{o}sin\beta }{gcos\alpha }$

 

Motion along OX

x= L ,u_x= V_ocos $\beta$ , a_x= -gsin $\alpha$

t =T = $\frac{2V_{o}sin\beta }{gcos\alpha }$

x= u_xt+ $\frac{1}{2}{a}_x{t}^2$

L= V₀cos $\beta T$ + $\frac{1}{2}(-gsin\alpha )T^2$

L= T[V₀cos $\beta -\frac{1}{2}gsin\alpha T$ ]

L=  $\frac{2V_{o}sin\beta }{gcos\alpha }$ [V_ocos $\beta -\frac{V_{o}sin\alpha sin\beta }{cos\alpha }$ ]

L= $\frac{2v_o^{2}sin\beta }{g{cos}^2\alpha }\mathrm{c}\mathrm{o}\mathrm{s}?\left(\alpha +\beta \right)$

Z= sin $\beta \mathrm{c}\mathrm{o}\mathrm{s}?\left(\alpha +\beta \right)$

 = sin $\beta [cos\alpha cos\beta -sin\alpha sin\beta ]$

= $\frac{1}{2}(cos\alpha +sin2\beta -2sin\alpha .{sin}^2\beta )$

= ½ [sin2] $\beta cos\alpha -sin\alpha (1-cos2\beta )$

= $\frac{1}{2}[sin2\beta cos\alpha +cos2\beta .sin\alpha -sin\alpha ]$

= $\frac{1}{2}$  [sin(2 $\beta +\alpha$ )-sin $\alpha$ ]

For z maximum

2 $\beta +\alpha =\frac{\pi }{2}$  , $\beta =\frac{\pi }{4}-\frac{\alpha }{2}$

This is a Long Answer Type Question as classified in NCERT Exemplar

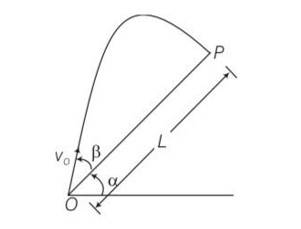
Explanation – target T is at horizontal distance x= R+ $?x$ and between point of projection y= -h

Maximum horizontal range R= $\frac{v_o^2}{g}\theta =45$ …………1

Horizontal component of initial velocity = V_ocos $\theta$

Vertical component of initial velocity = -V_osin $\theta$

So h = (-V_osin $\theta$ )t + $\frac{1}{2}gt$ ²………….2

R+ $?x$  = V_ocos $\theta *t$

So t= $\frac{R+?x}{v_{o}cos\theta }$

Substituting value of t in 2 we get

So h = (-V₀sin $\theta$ ) $\left(\mathrm{}\frac{R+?x}{v_{o}cos\theta }\right)+\frac{1}{2}g({\mathrm{}\frac{R+?x}{v_{o}cos\theta })}^2$

H = -(R+ $?x$ )tan $\theta$ + $\frac{1}{2}g\left(\frac{({R+?x)}^2}{v_o^2{cos}^2\theta }\right)$

$\theta =45$ ,  h = -(R+ $?x$ )tan $45$ + $\frac{1}{2}g\left(\frac{({R+?x)}^2}{v_o^2{cos}^{2}45}\right)$

So h = -(R+ $?x$ ) $1$ + $\frac{1}{2}g\left(\frac{({R+?x)}^2}{v_o^2\left(\frac{1}{2}\right)}\right)$

So h = -(R+ $?x$ )+ $\frac{{(R+?x)}^2}{R}$

So h = -R- $?x$ +(R+ $\frac{{?x}^2}{R}+2?x$ )

 h= $?x+\frac{{?x}^2}{R}$

This is a Long Answer Type Question as classified in NCERT Exemplar

Explanation- speed of jackets = 125m/s

Height of hill = 500m

To cross the hill vertical component of velocity should be grater than this value u_y= $\sqrt[]{2gh}$

$=\sqrt[]{2*10*500}=100m/s$

So u²= u_x²+u_y²

Horizontal component of initial velocity u_x = $\sqrt[]{u^2-u_y^2}=\sqrt[]{{125}^2-{100}^2}=75m/s$

Time taken to reach the top of hill t= $\sqrt[]{\frac{2h}{g}}=\sqrt[]{\frac{2*500}{10}}=10s$

Time taken to reach the ground in 10 sec = 75 (10)= 750m

Distance through which the canon has to be moved =800-750=50m

Speed with which canon can move = 2m/s

Time taken canon = 50/2= 25s

Total time t= 25+10+10= 45s