Physics NCERT Exemplar Solutions Class 11th Chapter Four

Given

$I=\frac{2E}{R=r_1+r_2}$

E₁ = E₂ = E - (i)

Potential drop across second cell is

$V_A-E_2+I{r}_2=v_B$

According to question VA – VB = 0

E2 lr2 = 0

$\Rightarrow R=r_2-r_1$

Linear motion is one-dimensional motion. It refers to motion in a single direction or in a straight line. In linear motion, the object either moves forward or backward along one axis, i.e. x-axis. For example - a ball dropped from a height vertically downward or a car moving straight on a road. Motion in a Plane refers to an object moving in two dimensions, usually along x and y axes. For example, a football kicked at an angle.

The angle of projection is used to find the trajectory, horizontal range of a projectile, maximum height, and time of flight. For example, the maximum range on level ground is given by the 45-degree angle.

The vectors like velocity, displacement, and acceleration act along different directions in the two-dimensional motion. Resolving the vectors into the vertical and horizontal components allows the application of one-dimensional kinematic equations in each direction separately. It helps solve the problems more accurately and also simplifies the analysis.

This is a Multiple Choice Questions as classified in NCERT Exemplar

Explanation- |A+B|=|A-B|

$\sqrt[]{\left|{A|}^2+\left|{B|}^2+2\right|A\right|\left|B\right|cos\theta }=\sqrt[]{\left|{A|}^2+\left|{B|}^2-2\right|A\right|\left|B\right|cos\theta }$

$\left|{A|}^2+\left|{B|}^2+2\right|A\right|\left|B\right|cos\theta$  = $\left|{A|}^2+\left|{B|}^2-2\right|A\right|\left|B\right|cos\theta$

4|A|B|cos $\theta$ =0

|A|²+|B|²cos $\theta$ =0

A=0 or B=0 so $\theta =90$ . so A perpendicular B

This is a Multiple Choice Questions as classified in NCERT Exemplar

Answer- a, b, c

Explanation- (i) speed will constant throughout

(ii) velocity will be tangential in the direction of motion

(iii) centripetal acceleration will be a= v²/r, will always be towards centre of the circular path.

(iv) angular momentum is constant in magnitude and direction out of the plane perpendicularly as well.

This is a Multiple Choice Questions as classified in NCERT Exemplar

Answer- a, c

Explanation – as we know average acceleration is a_av= $\frac{?v}{?t}=\frac{v_2-v_1}{t_2-t_1}$

But when acceleration is not uniform V_av is not equal to v₁+v₂/2

So we can write $?v=\frac{?r}{?t}$

$?r=r_2-r_1$ = v₂-v₁ (t₂-t₁)

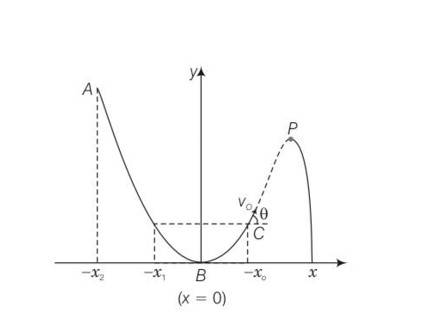
This is a Multiple Choice Questions as classified in NCERT Exemplar

Answer- c

Explanation– as the given track y=x² is a frictionless track thus total energy will be same throughout the journey.

Hence total energy at A = total energy at P . at B the particle is having only Ke but at P some KE is converted to P

Hence (KE)_B = (KE)_P

Total energy at A = PE= total energy at B = KE= total energy at P

= PE+KE

Potential energy at A is converted to KE and PE at P hence

(PE)P< (PE)A

Hence (height)P= (height)A

As height of p < height of A

Hence path length AB > path length BP

This is a Multiple Choice Questions as classified in NCERT Exemplar

Answer- a,b,c

Explanation – H= $\frac{u^2{sin}^2\theta }{2g}$

H₁=V_o²sin^{2 $\theta$} ₁/2g  , H₂=V_o²sin^{2 $\theta$} ₂/2g

H₁>H₂

V_o²sin^{2 $\theta$} ₁/2g= V_o²sin^{2 $\theta$} ₂/2g

Sin^{2 $\theta$} ₁>sin^{2 $\theta$} ₂

Sin^{2 $\theta$} ₁ – sin² $\theta$ ₂>0

(Sin $\theta$ ₁ – sin $\theta$ ₂)( Sin $\theta$ ₁ + sin $\theta$ ₂)>0

Sin $\theta$ ₁>sin $\theta$ ₂ or ₁ >₂

T= $\frac{2usin\theta }{g}=\frac{2v_{o}sin\theta }{g}$

T₁= $\frac{2v_{o}sin{\vartheta }_1}{g}$   , T₂= $\frac{2v_{o}sin{\vartheta }_2}{g}$

T₁> T₂

R= $\frac{u^{2}sin2\theta }{g}=\frac{v_o^{2}sin2\theta }{g}$

Sin $\theta$ ₁>sin $\theta$ ₂

Sin2 $\theta$ ₁> sin2 $\theta$ ₂

$\frac{R_1}{R_2}=\frac{\mathrm{S}\mathrm{i}\mathrm{n}2{\theta }_1}{sin2{\theta }_2}1$

R₁>R₂

Total energy for the first particle

U₁=K.E+P.E=1/2m_{1 $v_o^2$}

U₂= K.E+P.E= 1/2m_{2 $v_o^2$}

Total energy for the second particle

So m₁= m₂ then U₁=U₂

So m₁>m₂ then U₁>U₂

So m₁2 then U1