Physics NCERT Exemplar Solutions Class 11th Chapter Four Motion in a Plane is a comprehensive practice material for Class 12 Science students who are planning to appear in Board exams and other competitive exams. The exemplar goes beyond the NCERT textbook and provides various types of questions about the key concepts of the Thermal Properties of Matter. These questions will be Multiple-Choice Questions, Very-Short Answer Type Questions, Short-Answer Type Questions, and Long Answer Type questions. After practicing these questions, students will improve their problem-solving skills. For a better understanding of the key topics of this chapter, the students should also refer to the Class 11 Physics Chapter 3 NCERT Solutions.
Students can also download the Motion in a Plane NCERT PDF from this page. The PDF has detailed explanations and step-by-step answers to all the questions of the NCERT Exemplar Physics Class 11 Chapter Four. These solutions are designed by the subject matter experts to reinforce theoretical understanding. By practicing these, students will gain more confidence in solving the complex questions of the chapter.
- Important Formulas Related to Physics Chapter Four NCERT Exemplar
- NCERT Exemplar Class 11 Physics Motion In a Plane Very Short Answer Type Questions
- Motion In a Plane NCERT Exemplar Class 11 Physics Short Answer Type Questions
- NCERT Exemplar Motion In a Plane Class 11 Physics Long Answer Type Questions
- Class 11 Physics NCERT Exemplar Motion In a Plane Objective Type Questions
- JEE Mains 2022
Important Formulas Related to Physics Chapter Four NCERT Exemplar
These are the important formulas of the Motion in a Plane:
Vector Addition and Subtraction
Resultant of two vectors
Direction of resultant vector
Projectile Motion
Time of flight
Maximum height
Horizontal range
Equation of trajectory
Uniform Circular Motion
Centripetal acceleration
Centripetal force
Relation between angular and linear velocity
Time period
Relative Velocity
Relative velocity of A with respect to B
More Related Links
| NCERT Solution | NCERT Class 11 Physics |
| NCERT Notes | NCERT Class 12 Physics |
NCERT Exemplar Class 11 Physics Motion In a Plane Very Short Answer Type Questions
Find below the solutions:
See Below VSA Questions
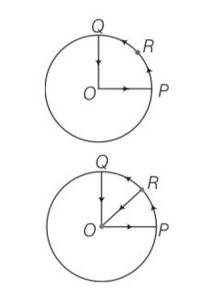
Q: A cyclist starts from centre O of a circular park of radius 1km and moves along the path OPRQO as shown Fig. 4.3. If he maintains constant speed of 10ms–1, what is his acceleration at point R in magnitude and direction?
A: Explanation- the cyclist covers OPRQO path.
As we know whenever an object performing circular motion, acceleration is called centripetal acceleration and is always directed towards the centre.
so there will be centripetal acceleration a= v2/r
So a= 100/1km= 100/1000=0.1m/s2 along RO.
A: Explanation- vsin = vertical component
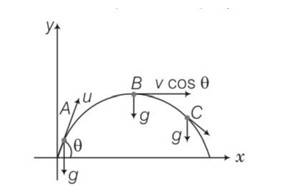
Vx= horizontal component of velocity =vcos = constant
Vy = vertical component of velocity =vsin
Velocity will always be tangential to the curve in the direction of motion and acceleration is always vertically downward and is equal to g.
Read more:
Commonly asked questions
A, B and C are three non-collinear, non co-planar vectors. What can you say about direction of A × (B × C)?
This is a Short Answer Type Question as classified in NCERT Exemplar
Explanation – the direction of (B ) will be perpendicular the plane containing B and B by right hand rule. A will lie in the plane of B and C and is perpendicular to vector A.
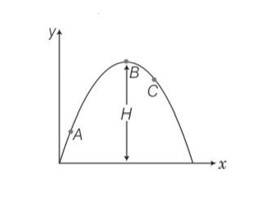
A ball is thrown from a roof top at an angle of 45° above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have
(a) Greatest speed.
(b) Smallest speed.
(c) Greatest acceleration? Explain
This is a Short Answer Type Question as classified in NCERT Exemplar
Explanation- at point B it will gain the same speed u and after that speed increases and will be maximum just before reaching point c.
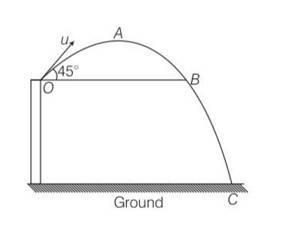
During journey from O to A speed decreases and will be maximum at point A and acceleration is always constant.
A football is kicked into the air vertically upwards. What is its (a) acceleration, and (b) velocity at the highest point?
This is a Short Answer Type Question as classified in NCERT Exemplar
Explanation- if the football is kicked into the air vertically upwards. Acceleration of football will always vertically downwards and equal to acceleration due to gravity. But when it reaches the highest point its velocity is zero and acceleration is retarding.
Motion In a Plane NCERT Exemplar Class 11 Physics Short Answer Type Questions
Here are the solutions:
Below Are SA Questions
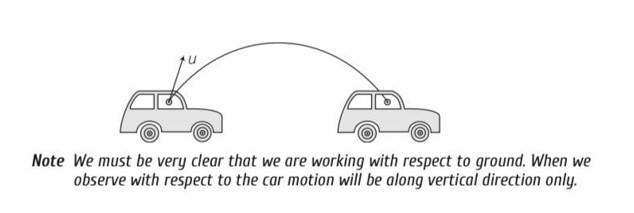
Q: A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give explanation to support your diagram.
A: This is a Short Answer Type Question as classified in NCERT Exemplar
Explanation – the path of the ball observed by a boy standing on the footpath is parabolic. The horizontal speed of the ball is same as that of the car, therefore ball as well car travels equal horizontal distance, due to vertical speed, the ball follows parabolic path.
This is a Short Answer Type Question as classified in NCERT Exemplar
Explanation – the boy throws the ball at an angle of 60.
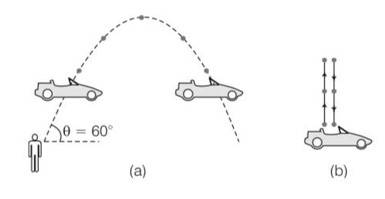
Horizontal component of velocity 4cos = 10cos60
=10 (1/2)
=5m/s.
so horizontal speed of the car is same, hence relative velocity of car and ball in the horizontal direction will be zero.
Commonly asked questions
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
This is a Short Answer Type Question as classified in NCERT Exemplar
Explanation – due to air resistance particle energy as well as horizontal component of velocity keep on decreasing making the fall steeper then rise. When we are neglecting air resistance path is parabola when we consider air resistance then path is asymmetric parabola.
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
This is a Short Answer Type Question as classified in NCERT Exemplar
Explanation- when it be at position P, drops a bomb to hit a target T
Let

Speed of the plane =720km/h = 720 = 200m/s
Altitude of the plane P’T = 1.5km= 1500m
If bomb hits the target after time t then horizontal distance travelled by the bomb PP’=u =200t
Vertical distance travelled by the bomb P’T=1/2gt2
1500 = ½ (9.8)t2
So t2= 1500/4.9, t =
PP’=200 (17.49)m=
tan =P’T/P’P=1500/200 (17.49)=0.49287= tan23012’
Given below in column I are the relations between vectors a, b and c and in column II are the orientations of a, b and c in the XY plane. Match the relation in column I to correct orientations in column II.
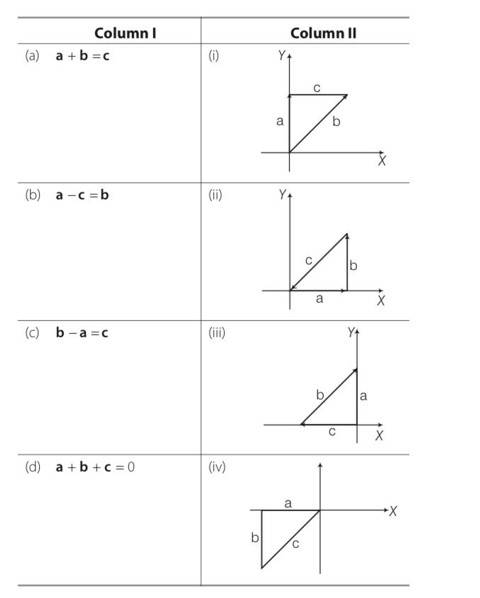
Explanation – here A and B vectors are joint by head and tail. So C= A+B
(a) from fig iv it is clear that c=a+b

(a) from fig iii it is clear that c+b=a so a-c=b
(b) from fig I it is clear that b=a+c so b-a =c
(c) from ii it is clear that -c= a+b so a+b+c=0
If A = 2 and B = 4, then match the relations in column I with the angle θ between A B and in column II. Column I Column II °

This is a Short Answer Type Question as classified in NCERT Exemplar
Explanation- given |A|=2 and |B|=4
a)|A |=AB sin = 0
so 2 sin =0
so so it matches with iv
B) |A B|= ABsin =8
2 sin =8
So = 90 so it matches with option iii
c) |A B|= ABsin =4
so =30 so it matches with option i
d) |A B|= ABsin =4
so =45 so it matches with option ii
If A = 2 and B = 4, then match the relations in column I with the angle θ between A B and in column II. Column I Column II °

This is a Short Answer Type Question as classified in NCERT Exemplar
Explanation- given |A|=2 and |B|=4
a)|A |=AB cos = 0
so 2 cos =0
so so it matches with ii
B) |A B|= ABcos =8
2 cos =8
So = 0 so it matches with option i
c) |A B|= ABcos =4
so =60 so it matches with option iv
d) |A B|= ABcos =-8
so =180 so it matches with option iii
NCERT Exemplar Motion In a Plane Class 11 Physics Long Answer Type Questions
See Below LA Questions
Q: A hill is 500 m high. Supplies are to be sent across the hill using a canon that can hurl packets at a speed of 125 m/s over the hill. The canon is located at a distance of 800m from the foot of hill and can be moved on the ground at a speed of 2 m/s; so that its distance from the hill can be adjusted. What is the shortest time in which a packet can reach on the ground across the hill ? Take g =10 m/s2.
A:
This is a Long Answer Type Question as classified in NCERT Exemplar
Explanation- speed of jackets = 125m/s
Height of hill = 500m
To cross the hill vertical component of velocity should be grater than this value uy=
So u2= ux2+uy2
Horizontal component of initial velocity ux =
Time taken to reach the top of hill t=
Time taken to reach the ground in 10 sec = 75(10)= 750m
Distance through which the canon has to be moved =800-750=50m
Speed with which canon can move = 2m/s
Time taken canon = 50/2= 25s
Total time t= 25+10+10= 45s
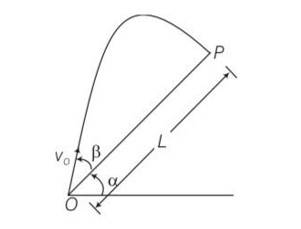
Q: A gun can fire shells with maximum speed vo and the maximum horizontal range that can be achieved is R= .If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Fig), show that it could be achieved by raising the gun to a height at least h =
A:
This is a Long Answer Type Question as classified in NCERT Exemplar
Explanation – target T is at horizontal distance x= R+ and between point of projection y= -h
Maximum horizontal range R= …………1
Horizontal component of initial velocity = Vocos
Vertical component of initial velocity = -Vosin
So h = (-Vosin )t + 2…………..2
R+ = Vocos
So t=
Substituting value of t in 2 we get
So h = (-V0sin )
H = -(R+ )tan +
, h = -(R+ )tan +
So h = -(R+ ) +
So h = -(R+ )+
So h = -R- +(R+ )
h=
Commonly asked questions
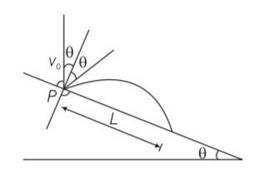
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Fig).
(a) Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
(b) Time of flight.
(c) β at which range will be maximum.
This is a Long Answer Type Question as classified in NCERT Exemplar
Explanation – particle is projected from the point O.
Let time taken in reaching from point O to point P is T.
for journey O to P
y=0,uy= Vosin ,ay= -gcos
y=uyt +

0= Vosin
T[Vosin T]=0
T = time of flight =
Motion along OX
x= L ,ux= Vocos , ax= -gsin
t =T =
x= uxt+
L= V0cos +
L= T[V0cos ]
L= [Vocos ]
L=
Z= sin
= sin
=
= ½ [sin2]
=
= [sin(2 )-sin ]
For z maximum
2 ,
A particle falling vertically from a height hits a plane surface inclined to horizontal at an angle θ with speed Vo and rebounds elastically . Find the distance along the plane where if will hit second time.
This is a Long Answer Type Question as classified in NCERT Exemplar
Explanation- y=O, uy= Vocos
ay=-gcos , t =T
applying equation of kinematics
y=uyt+ t2
0 = Vocos +T2
T=

T= 2V0/g
X= L, ux=Vosin , ax= gsin , t=T=
X=uxt+
L= Vosin
L= sin
A girl riding a bicycle with a speed of 5 m/s towards north direction, observes rain falling vertically down. If she increases her speed to 10 m/s, rain appears to meet her at 45° to the vertical. What is the speed of the rain? In what direction does rain fall as observed by a ground based observer?
This is a Long Answer Type Question as classified in NCERT Exemplar
Explanation – Vr= a? +b?
Velocity vg= 5m/s
Velocity of rain w.r.t girl = Vr-Vg= a? +b? -5?
= (a-5)? +b?
a-5=0, a=5
case II
vg = 10m/s?
Vrg= Vr - Vg
= a? +b? -10? = (a-10)? +b?
Rain appear to be fall at 45 degree so = b/a-10 =1
So b =-5
Velocity of rain = a? +b?
Vr = 5? -5?
Speed of rain Vr=
A river is flowing due east with a speed 3m/s. A swimmer can swim in still water at a speed of 4 m/s .
(a) If swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction)?
(b) If he wants to start from point A on south bank and reach opposite point B on north bank,
(a) Which direction should he swim?
(b) What will be his resultant speed?
(c) From two different cases as mentioned in (a) and (b) above, in which case will he reach opposite bank in shorter time?

This is a Long Answer Type Question as classified in NCERT Exemplar
Explanation – speed of river Vr= 3m/s
Speed of swimmer Vs= 4m/s
(a) when swimmer starts swimming due north then its resultant velocity
V=
tan so ’N
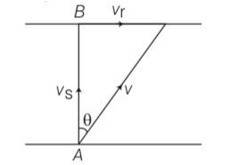
(b) to reach at point B resultant velocity will be
V=
tan

(c) time taken by swimmer t =d/v= d/4s
in case b time taken by swimmer to cross the river
t1=d/v=d/
so t
A cricket fielder can throw the cricket ball with a speed vo . If he throws the ball while running with speed u at an angle θ to the horizontal, find
(a) The effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
(b) What will be time of flight?
(c) What is the distance (horizontal range) from the point of projection at which the ball will land ?
(d) Find q at which he should throw the ball that would maximise the horizontal range as found in (iii).
(e) How does q for maximum range change if u >vo , u = vo , u < vo?
(f) How does q in (v) compare with that for u = 0 (i.e.450) ?
This is a Long Answer Type Question as classified in NCERT Exemplar
Explanation- a) for x direction ux= u+vocos
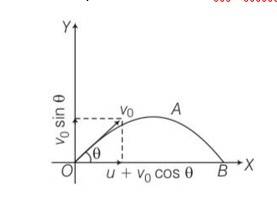
uy=velocity in y direction= v0sin
now tan
b) let t be the time flight y =0 uy=vosin
y= uyt+1/2 ayt2
0= vosin +
So T =
c) horizontal range R, = (u+vocos T= (u+vocos )
d) for range to be maximum dR/d
4vocos2
So cos =
e) cos =
so
f) if u=0 0
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in Cartesian co-ordinates where are unit vector along x and y directions, respectively and Ax and Ay are corresponding components of (Fig). Motion can also be studied by expressing vectors in circular polar co-ordinates as A=Arr + where ? =r/r=cos and are unit vectors along direction in which ‘r’ and ‘q ’ are increasing.
(a) Express in terms of q.
(b) Show that both q are unit vectors and are perpendicular to each other.
(c) Show that d(r)/dt , where w =dq/dt q and dq/dt = -wr
(d) For a particle moving along a spiral given by r=aqr , where a = 1 (unit), find dimensions of ‘a’.
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
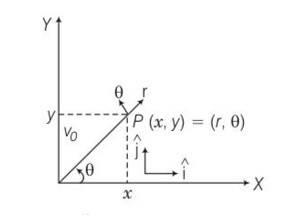
This is a Long Answer Type Question as classified in NCERT Exemplar
Explanation – r=cos ?……..1
…….2
Multiplying eq1 by sin and 2 with cos and adding
Rsin
= ?( )=j
= rsin
n(rcos )=i
b)r
= -cos
c)r=cos
dr/dt=d/dt(cos )=w[-cos ]
d)L= MoLT0
e)a=1unit , r=
v= dr/dt=
v=
= w
a=
a=
=
A man wants to reach from A to the opposite corner of the square C (Fig. 4.10). The sides of the square are 100 m. A central square of 50m × 50m is filled with sand. Outside this square, he can walk at a speed 1 m/s. In the central square, he can walk only at a speed of v m/s (v < 1). What is smallest value of v for which he can reach faster via a straight path through the sand than any path in the square outside the sand?
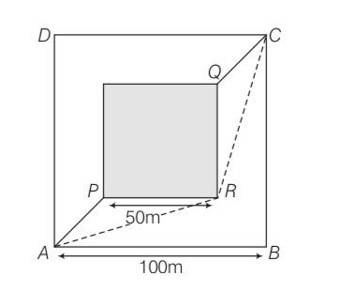
This is a Long Answer Type Question as classified in NCERT Exemplar
Explanation – Tsand=

= 50
Time taken Toutside=
AR=
RC= AR=
Toutside= 2AR= 50
Tsand
Class 11 Physics NCERT Exemplar Motion In a Plane Objective Type Questions
See Below MCQs
Commonly asked questions
The angle between A= ? + ? and B = ? - ? is
(a) 45° (b) 90° (c) –45° (d) 180°
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- b
Explanation-A = i+j
B = i-j
A.B=|A|B|cos
(? +? ). (? -? ) = cos
Where is the angle between A and B
Cos = =
= 90o
Shows the orientation of two vectors u and v in the XY plane. If u = a? + b? and
v=p ? + q ? . which of the following is correct?
(a) a and p are positive while b and q are negative.
(b) a, p and b are positive while q is negative.
(c) a, q and b are positive while p is negative.
(d) a, b, p and q are all positive.
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- b

Explanation – u= a? + b? as u in the first quadrant, hence both components a and b will be positive. For v= p? + q? , as it is positive x direction and located downward hence x component p will be positive and y component q will be negative.
It is found that |A+B|=|A|. this necessarily implies.
(a) B=0
(b) A,B are antiparallel
(c) A,B are perpendicular
(d) A.B<0
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- a, b
Explanation - |A+B|= |A|or |A+B|2=|A|2
|A|2 +|B|2+2|A|B|cos = |A|2
|B| (|B|+2|A|cos )= 0
|B|=0 or |B|+2|A|cos =0
Cos =
If A and B are antiparallel then =180
-1=
Following are four different relations about displacement, velocity and acceleration for the motion of a particle in general. Choose the incorrect one (s) :
(a) Vav=
(b) Vav=
(c) Vav=
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- a, c
Explanation – as we know average acceleration is aav=
But when acceleration is not uniform Vav is not equal to v1+v2/2
So we can write
= v2-v1 (t2-t1)
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
(a) Magnitude of particle velocity (speed) remains constant.
(b) Particle velocity remains directed perpendicular to radius vector.
(c) Direction of acceleration keeps changing as particle moves.
(d) Angular momentum is constant in magnitude but direction keeps changing.
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- a, b, c
Explanation- (i) speed will constant throughout
(ii) velocity will be tangential in the direction of motion
(iii) centripetal acceleration will be a= v2/r, will always be towards centre of the circular path.
(iv) angular momentum is constant in magnitude and direction out of the plane perpendicularly as well.
For two vectors A and B, A B A B + = − is always true when (a) A B = ≠ 0 (b) A⊥ B (c) A B = ≠ 0 and A and B are parallel or anti parallel (d) when either A or B is zero.
This is a Multiple Choice Questions as classified in NCERT Exemplar
Explanation- |A+B|=|A-B|
=
4|A|B|cos =0
|A|2+|B|2cos =0
A=0 or B=0 so . so A perpendicular B
Which one of the following statements is true?
(a) A scalar quantity is the one that is conserved in a process.
(b) A scalar quantity is the one that can never take negative values.
(c) A scalar quantity is the one that does not vary from one point to another in space.
(d) A scalar quantity has the same value for observers with different orientations of the axes.
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- d
Explanation- a scalar quantity is independent of direction hence has the same value for observers with different orientations of the axes.
The component of a vector r along X-axis will have maximum value if
(a) r is along positive Y-axis
(b) r is along positive X-axis
(c) r makes an angle of 45° with the X-axis
(d) r is along negative Y-axis
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- b
Explanation – ler r makes an angle with positive x axis component if r along x-axis.
So rx= |r|cos
(rx)maximum= |r| (cos )maximum
= |r|cos = r
=00
R is along positive x-axis.
The horizontal range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same speed at an angle of 45°, its range will be
(a) 60 m
(b) 71 m
(c) 100 m
(d) 141 m
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- c
Explanation - we know that =150 and R= 50m
Range, R=
50 =
So u2= 980
So u = m/s
So u= 14 = 31.304m/s
= 450, R=
R= = =
Consider the quantities, pressure, power, energy, impulse, gravitational potential, electrical charge, temperature, area. Out of these, the only vector quantities are
(a) Impulse, pressure and area
(b) Impulse and area
(c) Area and gravitational potential
(d) Impulse and pressure
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- b
Explanation – we know that impulse J= f. = , where F is force . is time duration and is change in momentum. As is a vector quantity, hence impulse is also a vector quantity. Sometimes area can also be treated as vector.
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
(a) The average velocity is not zero at any time.
(b) Average acceleration must always vanish.
(c) Displacements in equal time intervals are equal.
(d) Equal path lengths are traversed in equal intervals.
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- d
Explanation – speed = total distance travelled /time taken
Total distance travelled = path length
= speed time
We should be very careful with the fact, that speed is related with total distance covered not with displacement.
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
(a) The acceleration of the particle is zero.
(b) The acceleration of the particle is bounded.
(c) The acceleration of the particle is necessarily in the plane of motion.
(d) The particle must be undergoing a uniform circular motion.
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer-b, d
Explanation- as given motion is two-dimensional motion and given that instantaneous speed vo is positive constant. Acceleration is rate of change of velocity. hence it will also be in the plane of motion.
It is found that |A+B|=|A|. This necessarily implies,
(a) B = 0
(b) A,B are antiparallel
(c) A,B are perpendicular
(d) A.B ≤ 0
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- b, d
Explanation – given A+B+C = 0
B
B +B =0
B
B
A
(A )
It cannot be zero
(b) (A ).C= (B ).C=0 . if b|C then B =0 then (B )
(c) (A )=X=ABsin . The direction of X is perpendicular to the plane containing A and B (A )
(d) if c2= A2+B2, then angle between A and B is 900
(A ).C= (AB sin900X).C=AB (X.C)
= ABC cos900= 0
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
(a) Angle of projection : q1 > q2
(b) Time of flight : T1 > T2
(c) Horizontal range : R1 > R2
(d) Total energy : U1 > U2 .
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- a,b,c
Explanation – H=
H1=Vo2sin2 1/2g , H2=Vo2sin2 2/2g
H1>H2
Vo2sin2 1/2g= Vo2sin2 2/2g
Sin2 1>sin2 2
Sin2 1 – sin2 2>0
(Sin 1 – sin 2)( Sin 1 + sin 2)>0
Sin 1>sin 2 or 1 >2
T=
T1= , T2=
T1> T2
R=
Sin 1>sin 2
Sin2 1> sin2 2
R1>R2
Total energy for the first particle
U1=K.E+P.E=1/2m1
U2= K.E+P.E= 1/2m2
Total energy for the second particle
So m1= m2 then U1=U2
So m1>m2 then U1>U2
So m1
A particle slides down a frictionless parabolic (y + x2 ) track (A – B – C) starting from rest at point A (Fig. 4.2). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
(a) KE at P = KE at B
(b) Height at P = height at A
(c) Total energy at P = total energy at A
(d) Time of travel from A to B = time of travel from B to P.
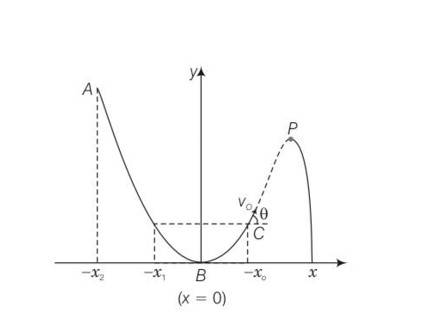
This is a Multiple Choice Questions as classified in NCERT Exemplar
Answer- c
Explanation– as the given track y=x2 is a frictionless track thus total energy will be same throughout the journey.
Hence total energy at A = total energy at P . at B the particle is having only Ke but at P some KE is converted to P
Hence (KE)B = (KE)P
Total energy at A = PE= total energy at B = KE= total energy at P
= PE+KE
Potential energy at A is converted to KE and PE at P hence
(PE)P< (PE)A
Hence (height)P= (height)A
As height of p < height of A
Hence path length AB > path length BP
JEE Mains 2022
JEE Mains 2022
Commonly asked questions
A car is moving with speed of 150 km/h and after applying the break it will move 27m before it stops. If the same car is moving with a speed of one third the reported speed then it will stop after travelling _________m distance.
Stopping distance =
If speed is made
Braking acceleration Remains same.
Four forces are acting at a point P in equilibrium as shown in figure. The ratio of force F1 to F2 is 1: x where x = _________.
x = 3
A wire of length L and radius r is clamped rigidly at one end. When the other end of the wire is pulled by a force F, its length increases by 5cm. Another wire of the same material of length 4L and radius 4r pulled by a force 4F under same conditions. The increases in length of this wire is _________cm.
=
A unit scale is to be prepared whose length dows not change with temperature and remains 20cm, using a bimetallic strip made of bass and iron each of different length. The length of both components would change in such a way that difference between their length remains constant. If length of brass is 40cm and length of iron will be ________cm.
An observer is riding on a bicycle and moving towards a hill at 18 kmh-1. He hears a sound from a source at some distance behind him directly as well as after its reflection from the hill. If the original frequency of the sound as emitted by source is 640 Hz and velocity of the sound in air is 320 m/s, the beat frequency between the two sounds heard by observer will be _________ Hz.
The volume charge density of a sphere of radius 6m is 2 The number of lines of force per unit surface area coming out from the surface of the sphere is _________ × 1010 NC-1.
[Given : Permittivity of vacuum
No. of electric field line per unit area = electric field
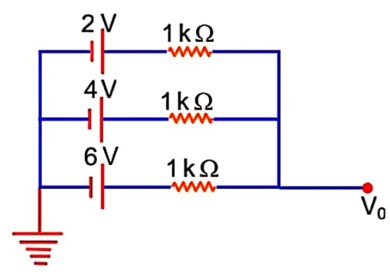
In the given figure, the value of V0 will be ________ V.
K V L Loop 1
6 - l × 1 -l1 × 1 - 4 = 0
2 = l + l1 - (i)
K V L Loop 2
4 + l1 × 1 - (l – l1) × 1 – 2 = 0
l = 2 + 2l1 - (ii)
from (i) & (ii)
l1 = 0 v0 = 4
Eight copper wire of length and diameter d are joined in parallel to from a single composite conductor of resistance R. If a single copper wire of length 2 have the same resistance (R) then its diameter will be ________d.
Each wile has resistance =
Eight wire in parallel, then equivalent resistance is
Single copper wire of length has resistance
d1 = 4d
The energy band gap of semiconducting material to produce violet (wavelength = 4000 ) LED is ________ eV. (Round off to the nearest integer).
The required height of a TV tower which can cover the population of 6.03 lakh is h. If the average population density is 100 per square km and the radius of earth is 6400 km, then the value of h will be ________ m.
Area =
km2
h = 150m
Physics NCERT Exemplar Solutions Class 11th Chapter Four Exam