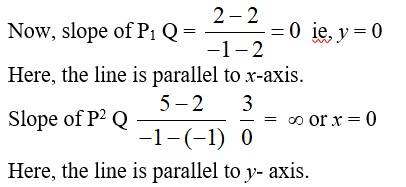Straight Lines
Get insights from 177 questions on Straight Lines, answered by students, alumni, and experts. You may also ask and answer any question you like about Straight Lines
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
70. The given equation of the line is
l1: x + y = 4
Let P (x0, y0) be the point of intersect of l1 and the line to be drawn.
Then, x0 + y0 = 4 ⇒ y0 = 4? x
Given, distance between P (x0, y0) and Q (? 1, 2) is 3
ie, ![]()
⇒ (x0 + 1)2 + (y? 2)2= 9
⇒x20+1+ 2x0 + (4? x? 2)2 = 9
⇒ x20+ 2x0 + 1 + (2? x0 )2 = 9
⇒x20+ 2x0 + 1 + 4 + x20 ? 4x0 ?9 = 0
⇒ 2 x20 ?2x0 ? 4 = 0
x20 ? x0 ? 2 = 0
x20 + x0 ? 2x0 ? 2 = 0
x0 (x +1)? 2 (x0 +1) = 0
(x0 +1) (x0 ? 2) = 0
x0 = 2 and x0 =? 1
When, x0 = 2, y0 = 4 ?2 = 2.
and when x0 =? 1, y0 = y? (?1) =5.
The points of interaction of line l1which are at distance 3 unit
New answer posted
7 months agoContributor-Level 10
69.
The given eqn of the lines are.
4x + 7y + 5 = 0______ (1)
2x - y = 0 ______ (2)
Solving (1) and (2) we get,
4 x + 7 (2 x)+5 = 0
4x +14 x + 5= 0
x =
and y = 2x =
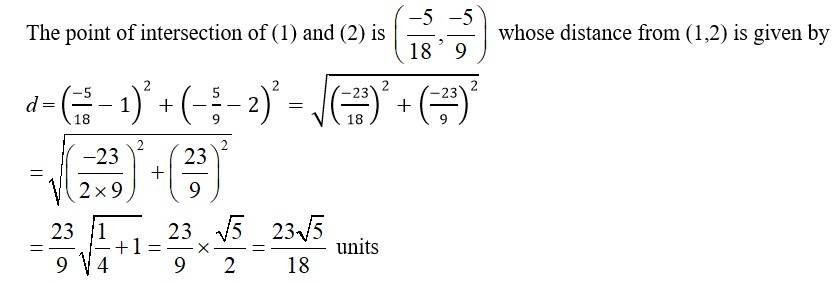
New answer posted
7 months agoContributor-Level 10
68. The given eqn of line is
l1: x + y = 4
Let R divides the line joining two points P (?1,1) and Q (5,7) in ratio k:1. Then,
Co-ordinate of R = ()
As l1 divides line joining PQ, then R lies on l1
i e, =4
5k ?1 + 7k + 1= 4 (k + 1)
12k = 4k + 4
8k = 4
k =
The ratio in which x + y = 4 divides line joining (?1,1) ad (5,7) is :1 i.e., 1: 2.
New answer posted
7 months agoContributor-Level 10
67. The given eqn of line is.
l1 : y = mx + c.
Slope of l1 = m
Let m? be the slope of line passing through origin (0, 0) and making angle θ with l1
Thus, (y 0) = m? (x 0)
y = m? x
m? =
______ (1)
And tanθ = =
When, tanθ =
tanθ + m? m tanθ = m' - m
m + tanθ = m? - m?m tanθ
m' =
When tan θ =
tan θ + m? m tanθ = -m? + m
m' =
Hence combining the two we get,
{-: eqn (1) }
New answer posted
7 months agoContributor-Level 10
66. The given eqn of the line is.
4x + 7y – 3 = 0 _____ (1)
2x – 3y + 1 = 0 _______ (2)
Solving (1) and (2) using eqn (1) 2 x eqn (2) we get,
(4x + 7y – 3) 2 [ (2x – 3y + 1)] = 0
4x + 7y – 3 – 4x + 6y – 2 = 0
13y = 5
y =
And 2x – 3 + 1 = 0
2x = – 1 =
Point of intersection of (1) and (2) is
Since, the line passing through has equal intercept say c then it is of the form
x + y = c
c =
the read eqn of line is x + y =
13x + 13y – 6 = 0
New answer posted
7 months agoContributor-Level 10
65. x – 2y = 3
y = - ______ (1)
Slope of line (1) is
Let the line through P (3, 2) have slope m
Then, angle between the line =
When, =>2m – 1 = 2 + m=> m = 3.
The eqn of line through (3, 2) is
y – 2 = 3 (x – 3) 3x – y – 7 = 0.
When = – 1=> 2m – 1 = – 2 – m =>3m = – 1 m =
The equation of line through (3,2) is,
y – 2 = (x – 3) => 3y – 6 = – X + 3
x + 3y – 9 = 0
New answer posted
7 months agoContributor-Level 10
64. The given eqn of the three lines are
y = m1 x + c1 ______ (1)
y = m2 x + c2 ______ (2)
y = m3 x + c3 ______ (3)
The point of intersection of (2) and (3) is given by.
y - y = (m2x + c2) - (m3 x + c3)
(m2 - m3) x = c3 - c2
Hence, y =
As the three lines are concurrent, the point of intersection of (2) and (3) lies on line (1) also
i e,
m1 (c2 - c3) - c1 (m2 - m3) + m2 c3 - m3 c2 = 0
m1 (c2 - c3) - m2 c1 + m3 c1 + m2 c3 - m3 c2 = 0
m1 (c2 - c3) + m2 (c3 - c1) + m3 (c1 - c2) = 0
New answer posted
7 months agoContributor-Level 10
63. The given eqn of the lines are.
3x + y - 2 = 0 _____ (1)
Px + 2y - 3 = 0 ______ (2)
2x - y - 3 = 0 _____ (3)
Point of intersection of (1) and (3) is given by,
(3x + y - 2) + (2x - y - 3) = 0
=> 5x - 5 = 0
=> x =
=> x = 1
So, y = 2 - 3x = 2 -3 (1) = 2 - 3 = 1.
i e, (x, y) = (1, -1).
As the three lines interests at a single point, (1, -1) should line on line (2)
i e, P * 1 + 2 * (-1)- 3 = 0
P - 2 - 3 = 0
P = 5
New answer posted
7 months agoContributor-Level 10
62.
The given eqn of the lines are
y - x = 0 _____ (1)
x + y = 0 ______ (2)
x - k = 0 ______ (3)
The point of intersection of (1) and (2) is given by
(y - x) - (x + y) = 0
⇒ y - x -x -y = 0
y = 0 and x = 0
ie, (0, 0)
The point of intersection of (2) and (3) is given by
(x + y) – (x – k) = 0
y + k = 0
y = –k and x = k
i.e, (k, –k)
The point of intersection of (3) and (1) is given by
x = k
and y = k
ie, (k, k).
Hence area of triangle whose vertex are (0, 0), (k, –k)
and (k, k) is

New answer posted
7 months agoContributor-Level 10
61. The given Eqn of the line is = 1 ______ (1)
so, Slope of line = -
The line ⊥ to line (1) say l2 has
Slope of l2 =
Let P (0, y) be the point of on y-axis where it is cut by the line (1)
Then,
y = 6
i.e, the point P has co-ordinate (0, 6)
Eqn of line ⊥ to and cuts y-axis at P (0,6) is
y – 6 = (x – 0)
3y – 18 = 2x
2x – 3y + 18 = 0
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers