Tags Straight Lines

Straight Lines

Get insights from 177 questions on Straight Lines, answered by students, alumni, and experts. You may also ask and answer any question you like about Straight Lines

Follow Ask Question

177

Questions

Discussions

Active Users

Followers

New answer posted

10 months ago

Straight Lines Class 11th

Let ABC be a triangle with A (-3, 1) and $∠ A C B = θ,$ $0 < θ < \frac{π}{2} .$ If the equation of the median through B is 2x + y – 3 = 0 and the equation of angle bisector of C is 7x – 4y – 1 = 0, then tanq is equal to:

0 Follower 13 Views

Vishal Baghel

Contributor-Level 10

Line BM : 2x + y = 3 Þ M (0, 3)

Line CD : 7x – 4y = 1 Þ C (3, 5)

Mirror image of A (-3, 1) in the line CD is $(\frac{13}{5}, \frac{- 11}{5})$ and it will lie on BC.

Slope of AC is 2/3

Slope of BC is 18.

$t a n θ = \frac{18 - \frac{2}{3}}{1 + 18 (\frac{2}{3})} = \frac{4}{3}$

where θ = $∠ A C B$

0 0

New answer posted

10 months ago

Straight Lines Class 11th

A 10 inches long pencil AB with mid point C and a small eraser P are placed on the horizontal top of a table such that PC = $\sqrt[]{5}$ inches and $∠ P C B = t a n^{- 1} (2) .$

The acute angle through which the pencil must be rotated about C so that the perpendicular distance between eraser and pencil becomes exactly 1 inch is:

0 Follower 18 Views

alok kumar singh

Contributor-Level 10

$t a n^{- 1} 2 = θ$

->tan q = 2

$s i n (θ - α) = \frac{1}{\sqrt[]{5}}$

->4 – 2 tanq = 1 + 2 tan a tan a = $\frac{3}{4}$

$α = t a n^{- 1} \frac{3}{4}$

0 0

New answer posted

10 months ago

Straight Lines Class 11th

Let A(, 2), B(, 6) and $C (\frac{α}{4}, - 2)$ be vertices of a $Δ A B C .$ If $(5, \frac{α}{4})$ is the circumcentre of $Δ A B C,$ then which of the following is NOT correct about $Δ A B C ?$

0 Follower 4 Views

Payal Gupta

Contributor-Level 10

Circumcentre (D) $\equiv (5, \frac{α}{4})$

${(5 - α)}^{2} + {(\frac{α}{4} + 2)}^{2} = {(5 - α)}^{2} + {(\frac{α}{4} - 6)}^{2} . . . . . . . . . . . . . . . (i)$

${(5 - \frac{α}{4})}^{2} + {(\frac{α}{4} + 2)}^{2} . . . . . . . . . . . . . . . . . . . . (i i)$

(i) $\frac{α}{4} + 2 = \pm (\frac{α}{4} - 6)$

(ii) 9 + 16 = 9 + 16

$\oplus \to x$

$(-) \to \frac{α}{2} = 4 \Rightarrow α = 8$

ar $(A B C) = 24$

2S = 24

R = 5, r = $\frac{Δ}{s} = \frac{24}{12} = 2$

0 0

New answer posted

10 months ago

Straight Lines Class 11th

Let m₁, m₂ be the slopes of two adjacent sides of a square of side a such that a²+ 11a + $3 (m_{1}^{2} + m_{2}^{2}) = 220 .$ If one vertex of the square is $(10 (c o s α - s i n α), 10 (s i n α + c o s α)),$ where $α \in (0, \frac{π}{2})$ and the equation of one diagonal is $(c o s α - s i n α) x + (s i n α + c o s α) y = 10,$ then $72 (s i n^{4} α + c o s^{4} α) + a^{2} - 3 a + 13$ is equal to

0 Follower 22 Views

Payal Gupta

Contributor-Level 10

$m_{1} m_{2} = - 1,$ for square a,b,c,d let

$A (10 (c o s α - s i n α), 10 (s i n α + c o s α))$

Diagonal : (cosα - sinα)x + (sinα + cosα)y = 10

BD (diagonal)

Dist. Of BD from A is

$\frac{| 10 {(c o s α - s i n α)}^{2} + 10 {(s i n α + c o s α)}^{2} - 10 |}{\sqrt[]{2}} = \frac{a}{\sqrt[]{2}}$

$\frac{10}{\sqrt[]{2}} = \frac{a}{\sqrt[]{2}} \Rightarrow a = 10$

Also, a²+ 11a + 3 $(m_{1}^{2} + m_{2}^{2}) = 220$

210 + 3 $(c m_{1}^{2} + m_{2}^{2}) = 220$

$m_{1}^{2} + m_{2}^{2} = \frac{10}{3}$

Also, m₁ m₂ = -1

m² + $\frac{1}{m^{2}} = \frac{10}{3}$

or $- \sqrt[]{3}, \frac{1}{\sqrt[]{3}}$

m = $\sqrt[]{3}, \frac{- 1}{\sqrt[]{3}}$

$m^{4} - \frac{10}{3} m^{2} + 1 = 0 \Rightarrow m^{2} = \frac{\frac{10}{3} \pm \sqrt[]{\frac{100}{9} - 4}}{2} - \frac{\frac{10}{3} \pm \frac{8}{3}}{2} = 3, \frac{1}{3}$

m = $\pm \sqrt[]{3}, \pm \frac{1}{\sqrt[]{3}}$

Diagonal AC:

$(s i n α + c o s α) x - (c o s α - s i n α) y$

=10 cos2α - 10cos2α = 0

Slope of AC = $\frac{s i n α + c o s α}{c o s α - s i n α} = \frac{t a n α + 1}{1 - t a n α} = t a n (α + \frac{π}{4}) α = 30 °$

FIGURE

? = $72 (\frac{1}{16} + \frac{9}{16}) + 100 - 30 + 13 = \frac{720}{16} + 83 = 128$

0 0

New answer posted

10 months ago

Straight Lines Class 11th

A circle touches both the y-axis and the line x + y = 0. Then the locus of its center is:

0 Follower 4 Views

alok kumar singh

Contributor-Level 10

$| h | = r a n d \frac{| h | + k_{1}}{\sqrt[]{2}} = r$

\frac{{(h + k)}^{2}}{2} = h^{2} \Rightarrow h^{2} = k^{2} + 2 h k

x^{2} - y^{2} = 2 x y

0 0

New answer posted

10 months ago

Straight Lines Class 11th

Let A(1, 1) B(-4, 3), C(-2, -5) be vertices of a triangle ABC, P be a point on side BC, and $Δ_{1} a n d Δ_{2}$ be the area of triangles APB and ABC, respectively. If $Δ_{1} : Δ_{2} = 4 : 7,$ then the area enclosed by the lines AP, AC and the x-axis is

0 Follower 29 Views

alok kumar singh

Contributor-Level 10

$\frac{Δ_{1}}{Δ_{2}} = \frac{| \begin{matrix} 1 & 1 & 1 \\ x & - 4 x - x & 1 \\ - 4 & 3 & 1 \end{matrix} |}{| \begin{matrix} 1 & 1 & 1 \\ - 4 & 3 & 1 \\ - 2 & - 5 & 1 \end{matrix} |} = \frac{4}{7}$

->14 x – 35 y = -95 …. (ii)

Solve (i) & (ii), x = $\frac{- 20}{7}, y = \frac{- 11}{7}$

$a r Δ A Q R$

$= \frac{1}{2} * 1 * 1 = \frac{1}{2}$

0 0

New answer posted

10 months ago

Straight Lines Class 11th

Let

A₁ = ${(x, y) : | x | \leq y^{2}, | x | + 2 y \leq 8} a n d$

A₂ = ${(x, y) : | x | + | y | \leq k} :$ If 27 (Area A₁) = 5 (Area A₂), then k is equal to:

0 Follower 2 Views

alok kumar singh

Contributor-Level 10

Required area (above x-axis)

$A_{1} = 2 \int_{0}^{4} (\frac{8 - x}{2} - \sqrt[]{x}) d x$

$= 2 (16 - \frac{16}{4} - \frac{8}{3 / 2}) = \frac{40}{3}$

and $A_{2} = 4 (\frac{1}{2} . k^{2}) = 2 k^{2}$

$∴ 27 . \frac{40}{3} = 5 . (2 k^{2})$

-> k = 6

for above x-axis.

0 0

New answer posted

10 months ago

Straight Lines Class 11th

Let $\frac{d y}{d x} = \frac{a x - b y + a}{b x + c y + a},$ where a, b, c, are constants, represent a circle passing through the point (2, 5). Then the shortest distance of the point (11, 6) from this circle is:

0 Follower 3 Views

alok kumar singh

Contributor-Level 10

$\frac{d y}{d x} = \frac{a x - b y + a}{b x + c y + a}$

$= b x d y + c y d y + a d y = a x d x - b y d x + a d x$

$= \frac{c y^{2}}{2} + a y - \frac{a x^{2}}{2} - a x + b x y = k$

$a x^{2} + a y^{2} + 2 a x - 2 a y = k$

$\Rightarrow x^{2} + y^{2} + 2 x - 2 y = λ$

Short distance of (11,6)

= $\sqrt[]{1 2^{2} + 5^{2}} - 5$

= 13 – 5

= 8

0 0

New answer posted

10 months ago

Straight Lines Class 11th

Let A(a, -2), B(a, 6) and $C (\frac{α}{4}, - 2)$ be vertices of a $Δ A B C .$ If $(5, \frac{α}{4})$ is the circumcentre of $Δ A B C,$ then which of the following is NOT correct about $Δ A B C ?$

0 Follower 4 Views

alok kumar singh

Contributor-Level 10

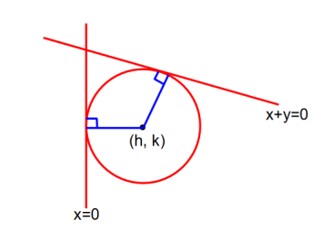
Circumcentre (D) $\equiv (5, \frac{α}{4})$

${(5 - α)}^{2} + {(\frac{α}{4} + 2)}^{2} = {(5 - α)}^{2} + {(\frac{α}{4} - 6)}^{2} . . . . . . . . . . . . . . . (i)$

${(5 - \frac{α}{4})}^{2} + {(\frac{α}{4} + 2)}^{2} . . . . . . . . . . . . . . . . . . . . (i i)$

(i) -> $\frac{α}{4} + 2 = \pm (\frac{α}{4} - 6)$

(ii) -> 9 + 16 = 9 + 16

$\oplus \to x$

$(-) \to \frac{α}{2} = 4 \Rightarrow α = 8$

ar $(A B C) = 24$

2S = 24

R = 5, r = $\frac{Δ}{s} = \frac{24}{12} = 2$

0 0

New answer posted

10 months ago

Straight Lines Class 11th

Let m₁, m₂ be the slopes of two adjacent sides of a square of side a such that a² + 11a + $3 (m_{1}^{2} + m_{2}^{2}) = 220 .$ If one vertex of the square is $(10 (c o s α - s i n α), 10 (s i n α + c o s α)),$ where $α \in (0, \frac{π}{2})$ and the equation of one diagonal is $(c o s α - s i n α) x + (s i n α + c o s α) y = 10,$ then $72 (s i n^{4} α + c o s^{4} α) + a^{2} - 3 a + 13$ is equal to:

0 Follower 14 Views

alok kumar singh

Contributor-Level 10

$m_{1} m_{2} = - 1,$ for square a,b,c,d let

$A (10 (c o s α - s i n α), 10 (s i n α + c o s α))$

Diagonal : (cos a - sina)x + (sina + cosa)y = 10

BD (diagonal)

Dist. Of BD from A is

$\frac{| 10 {(c o s α - s i n α)}^{2} + 10 {(s i n α + c o s α)}^{2} - 10 |}{\sqrt[]{2}} = \frac{a}{\sqrt[]{2}}$

$\frac{10}{\sqrt[]{2}} = \frac{a}{\sqrt[]{2}} \Rightarrow a = 10$

Also, a² + 11a + 3 $(m_{1}^{2} + m_{2}^{2}) = 220$

-> 210 + 3 $(c m_{1}^{2} + m_{2}^{2}) = 220$

$m_{1}^{2} + m_{2}^{2} = \frac{10}{3}$

Also, m₁ m₂ = -1

->m² + $\frac{1}{m^{2}} = \frac{10}{3}$

or $- \sqrt[]{3}, \frac{1}{\sqrt[]{3}}$

m = $\sqrt[]{3}, \frac{- 1}{\sqrt[]{3}}$

$m^{4} - \frac{10}{3} m^{2} + 1 = 0 \Rightarrow m^{2} = \frac{\frac{10}{3} \pm \sqrt[]{\frac{100}{9} - 4}}{2} - \frac{\frac{10}{3} \pm \frac{8}{3}}{2} = 3, \frac{1}{3}$

m = $\pm \sqrt[]{3}, \pm \frac{1}{\sqrt[]{3}}$

Diagonal AC:

$(s i n α + c o s α) x - (c o s α - s i n α) y$

=10 cos2a - 10cos2a = 0

Slope of AC = $\frac{s i n α + c o s α}{c o s α - s i n α} = \frac{t a n α + 1}{1 - t a n α} = t a n (α + \frac{π}{4}) α = 30 °$

...more

$m_{1} m_{2} = - 1,$ for square a,b,c,d let

$A (10 (c o s α - s i n α), 10 (s i n α + c o s α))$

Diagonal : (cos a - sina)x + (sina + cosa)y = 10

BD (diagonal)

Dist. Of BD from A is

$\frac{| 10 {(c o s α - s i n α)}^{2} + 10 {(s i n α + c o s α)}^{2} - 10 |}{\sqrt[]{2}} = \frac{a}{\sqrt[]{2}}$

$\frac{10}{\sqrt[]{2}} = \frac{a}{\sqrt[]{2}} \Rightarrow a = 10$

Also, a² + 11a + 3 $(m_{1}^{2} + m_{2}^{2}) = 220$

-> 210 + 3 $(c m_{1}^{2} + m_{2}^{2}) = 220$

$m_{1}^{2} + m_{2}^{2} = \frac{10}{3}$

Also, m₁ m₂ = -1

->m² + $\frac{1}{m^{2}} = \frac{10}{3}$

or $- \sqrt[]{3}, \frac{1}{\sqrt[]{3}}$

m = $\sqrt[]{3}, \frac{- 1}{\sqrt[]{3}}$

$m^{4} - \frac{10}{3} m^{2} + 1 = 0 \Rightarrow m^{2} = \frac{\frac{10}{3} \pm \sqrt[]{\frac{100}{9} - 4}}{2} - \frac{\frac{10}{3} \pm \frac{8}{3}}{2} = 3, \frac{1}{3}$

m = $\pm \sqrt[]{3}, \pm \frac{1}{\sqrt[]{3}}$

Diagonal AC:

$(s i n α + c o s α) x - (c o s α - s i n α) y$

=10 cos2a - 10cos2a = 0

Slope of AC = $\frac{s i n α + c o s α}{c o s α - s i n α} = \frac{t a n α + 1}{1 - t a n α} = t a n (α + \frac{π}{4}) α = 30 °$

FIGURE

? = $72 (\frac{1}{16} + \frac{9}{16}) + 100 - 30 + 13 = \frac{720}{16} + 83 = 128$

less

0 0

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

66k Colleges
1.2k Exams
695k Reviews
1850k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Need guidance on career and education? Ask our experts

Your Question

Straight Lines

Questions

Discussions

Active Users

Followers

All

Discussions

Unanswered Questions

Share Your College Life Experience