Straight Lines
Get insights from 177 questions on Straight Lines, answered by students, alumni, and experts. You may also ask and answer any question you like about Straight Lines
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
40.
The given equation of the line is.
12 (x + 6) = 5 (y- 2)
⇒ 12x + 72 = 5y- 9
⇒ 12x- 5y + 72 + 9 = 0
⇒ 12x- 5y + 82 = 0
The perpendicular distance of point (-1, 1) from the line is given by
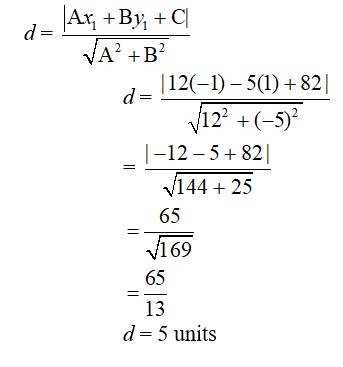
New answer posted
7 months agoContributor-Level 10


As w lies in IVth quadrant
Cos w = cos 45° and sin w = - sin 45°
= cos (360°- 45°) = sin (360°- 45°)
= cos 315° &nbs
New answer posted
7 months agoContributor-Level 10
38. (i) Given, 3x + 2y 12 = 0.
3x + 2y = 12
Dividing both sides by 12 we get,
Comparing the above equation with = we get, x-intercept, a = 4 and y-intercept b = 6.
(ii) Given, 4x - 3y = 6
Dividing the both sides by 6.
Comparing above equation by we get, x-intercept a = and y-intercept, b = -2
(iii) Given, 3y + 2 = 0.
3y = -2
As the equation of line is of form y = constant, it is parallel to x-axis and has no x-intercept.
y-intercept = -
New answer posted
7 months agoContributor-Level 10
Exercise 9.3
37. (i) Given, x + 7y = 0.
7y = -x
y = x + 0.
Comparing the above equation with y = mx + c we get, slope, m = - and c = 0, y-intercept
(ii) Given, 6x + 3y - 5 = 0
3y = -6x + 5
y = - x + = -2x +
Comparing the above equation with y = mx + c we get, slope, m = -2 and , y-intercept
(iii) Given, y = 0
y = 0xx + 0
Comparing the above equation with y = mx + c we get, Slope, m = 0 and c = 0, y-intercept.
New answer posted
7 months agoContributor-Level 10
36.
Let the given points be A (3, 0), B (–2, –2) and C (8, 2). Then by two point form we can write equation of line passing point A (3, 0) and B (–2, –2) as
If the three points A, B and C are co-linear, C will also lieonm the line formed by AB or satisfies equation (1).
Hence, putting x = 8 and y = 2 we have
L.H.S. = 2 * 8 – 5 * 2 – 6
= 16 – 10 – 6
= 0 = R.H.S.
The given three points are collinear.
New answer posted
7 months agoContributor-Level 10
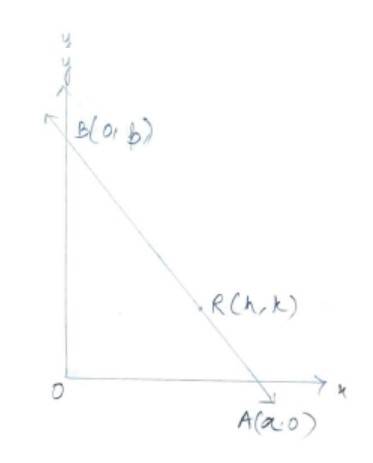
35. Equation of line with intercept form is
As R (h, x) divides line segment joining point A (a, 0) and B (0, b) in the ratio 1 : 2 we can write,
So,
Hence, putting value of a and b in equation (1) we get,
New answer posted
7 months agoContributor-Level 10
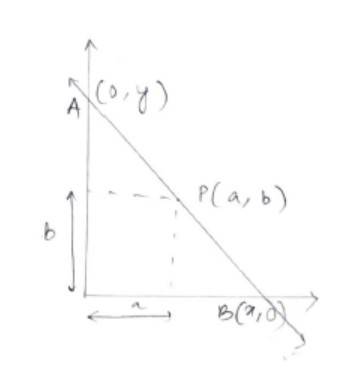
34.
Since P (a, b) is the mid-point of the line segment say AB with points A (0, y) and B (x, 0) we can write,
So, the equation of line with x and y intercept 2a and 2b using intercept form is
Hence, proved
New answer posted
7 months agoContributor-Level 10
33. Assuming the price per litre say P in x-axis and the corresponding demand say D in y-axis, we have two point (14, 980) and (16, 1220) in xy plane. Then the points (P, D) will satisfy the equation.
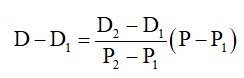
Which is the required relation
Where P = 17, we have
D = 120 * 17 – 700
D = 1340
Hence, the owner can sell 1340 litres of milk weekly at? 17/litre
New answer posted
7 months agoContributor-Level 10
32.
Since P (a, b) is the mid-point of the line segment say AB with points A (0, y) and B (x, 0) we can write,
So, the equation of line with x and y intercept 2a and 2b using intercept form is
Hence, proved
New answer posted
7 months agoContributor-Level 10
31.
Assuming the price per litre say P in x-axis and the corresponding demand say D in y-axis, we have two point (14, 980) and (16, 1220) in xy plane. Then the points (P, D) will satisfy the equation.
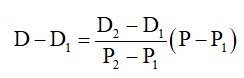
Which is the required relation
Where P = 17, we have
D = 120 * 17 – 700
D = 1340
Hence, the owner can sell 1340 litres of milk weekly at 17/litre
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers