System of Particles and Rotational Motion
Get insights from 71 questions on System of Particles and Rotational Motion, answered by students, alumni, and experts. You may also ask and answer any question you like about System of Particles and Rotational Motion
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Mass of the cylinder, m = 20 kg
Angular speed, = 100 rad/s
Radius of the cylinder, r = 0.25 m
The moment of inertia of the solid cylinder
I = (1/2) mr2 = (1/2) x 20 x (0.25)2 = 0.625 m2
Kinetic energy = (1/2)I 2 = (1/2) x 0.625 x (100)2 = 3125 J
Angular momentum, L = I = 0.625 x 100 = 62.5 Js
New answer posted
7 months agoContributor-Level 10
Let m and r be the mass and radius of the hollow cylinder and solid sphere.
The moment of inertia of the hollow cylinder about its standard axis, =I
The MI of the solid sphere about an axis passing through its centre, Is = (2/5) mr2
We know the relation = I , where
= angular acceleration
= torque
I = moment of inertia
For the hollow cylinder, =
For the solid sphere, =
Since the torque applied is same, = , we get
= = (mr2) /( (2/5) mr2 )) = 5/2
Hence ……(i)
Now using the relation
+ where
= initial angul
New answer posted
7 months agoContributor-Level 10
(a)
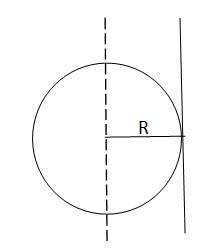
The moment of Inertia of a sphere about its diameter = 2MR 2/5
According to the theorem of parallel axis, the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and square of the distance between two parallel axes
Hence the moment of inertia about a tangent of the sphere = 2MR 2/5 + MR2 = 7MR 2/5
(b)
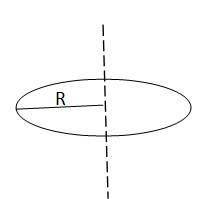
The moment of inertia of a disc about its diameter = MR 2/4
According to the theorem of perpendicular axis, the moment of inertia of a planar body about an axis perpendicular to its plane is equal to t
New answer posted
7 months agoContributor-Level 10

Mass of the car, m = 1800 kg
Distance between the front and rear axles, d = 1.8 m
Distance between C.G. and the front axle = 1.05 m
Let Rf and Rb be the force exerted from ground at front and rear axles respectively.
Rf + Rb = mg = 1800 x 9.8 N = 17640 N ……. (i)
For rotational equilibrium around C.G. we have Rf x 1.05 = Rb x (1.8 – 1.05)
Rf x 1.05 = Rb x 0.75
Rf/Rb = 0.75 / 1.05
Rf = 0.71 Rb ……. (ii)
From equation (i), we get
0.71 Rb + Rb = 17640
Rb = 10316 N
Rf = 7324 N
Therefore, force exerted on each front wheel = Rf/2 =7324/2 = 3662 N
Force exerted on each rear wheel, Rb/2 = 10316 / 2= 5158 N
New answer posted
7 months agoContributor-Level 10
A free body diagram needs to be drawn.
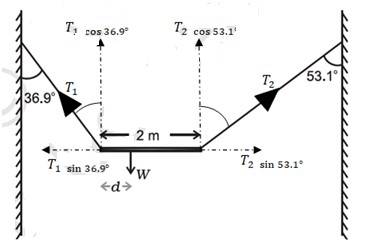
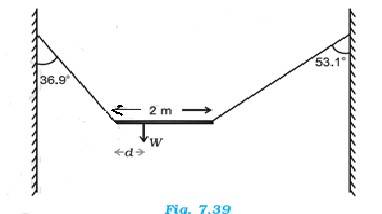
The length of the bar, l = 2 m
T1 and T2
At translational equilibrium, we have =
(T1 / T2) = ( / = 4/3
T1 = (4/3)T2
For rotational equilibrium, on taking the torque about the centre of gravity, we have
T1 x d = T2 (2-d)
T1 x 0.8d = T2 x 0.6 (2-d)
(4/3)T2 x 0.8d = T2 x 0.6 (2-d)
(4/3) x 0.8d = 0.6 (2-d)
1.07d = 1.2 – 0.6d
d = 0.72
So the c.g. of the given bar lies at 0.72 m from its left end.
New answer posted
7 months agoContributor-Level 10
Let at certain instant two particles be at points P and Q, as shown in the figure.
Angular momentum of the system about point P
= mv x 0 + mv x d = mvd ……. (i)
Angular momentum of the system about point Q
= mv x d + mv x 0 = mvd ……. (ii)
Consider a point R, which is at a distance y from point Q such that QR = y
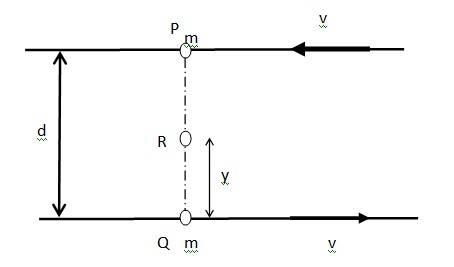
PR = d – y
Angular momentum of the system about point R
= mv x (d – y) + mv x y = mvd – mvy + mvy = mvd ……. (iii)
Comparing equations (i), (ii) and (iii) we get
= = …… (iv)
New answer posted
7 months agoContributor-Level 10
Let = , = , =
Let be a unit vector perpendicular to both b and c. Hence and a have the same direction
Now = bc
= bc = bc
Now )= a. (bc ) = abccos ? = abccos0° = abc = Volume of the parallelepiped
New answer posted
7 months agoContributor-Level 10
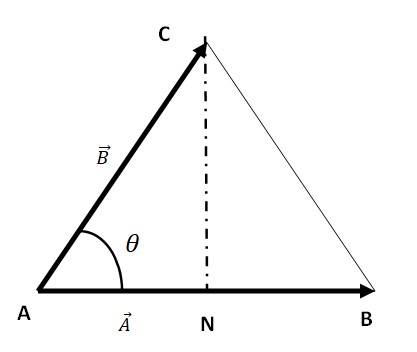
Let AB is equal to the vector a and AC be equal to the vector b.
Consider two vectors = =
= inclined at an angle
MN =
| | = | | |
The area of ΔABC, we can write the relation
Area of Δ ABC = AB =
New answer posted
7 months agoContributor-Level 10
The child is sitting on the trolley and there is no external force, hence it is a single system. The velocity of the centre of mass will not change, irrespective of any internal motion.
New answer posted
7 months agoContributor-Level 10
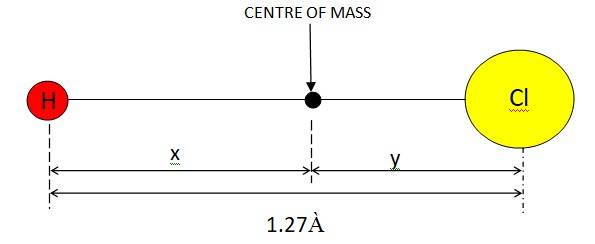
If mass of the H atom = m, mass of the Cl atom = 35.5m
Given x + y = 1,27 À
Let us assume that the centre of mass of the given molecule lies at the origin. Therefore,
We can have, : (my+35.5mx)/ (m+35.5m) = 0
mx + 35.5my = 0
x = 35.5 (1.27 – x)
x = 1.24 À
So the centre of mass lies 1.24 À from H atom
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers