Application of Derivatives
Get insights from 282 questions on Application of Derivatives, answered by students, alumni, and experts. You may also ask and answer any question you like about Application of Derivatives
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
The eqnof the given curve is
Slope of tangent,
(a) The line compared to gives,
Slope of line = 2.
If the tangent of the curve is parallel to the line
When
Hence, the point of contact of the tangent is (2, 7)
The eqn of tangent is
(b) The line
compared to gives
slope of line = 3
As the tangent to the curve is ⊥ to the line.
When we get
Hence, the point of contact of the tangent is
And eqn of the tangent is
New answer posted
7 months agoContributor-Level 10
(i) we have,
slope of tangent,
slope of normal
Hence eqn of tangent at (0, 5) is
And eqn of normal at (0, 5) is
(ii) We have,
Slope of tangent,
= 30 28
= 2
Slope of normal
Hence eqn of tangent at (1, 3) is
And eqn of normal at (1,3) is
(iii) We have,
Slope of tangent,
And slope of normal
Hence, eqn of tangent at (1, 1) is
And eqn of normal at (1,1) is
(iv) We have,
Slope of tangent
So, eqn of the tangent at (0,0) is
ie, x- axis
Hence, the eqn of normal is x = 0 ie, y-axis
(v) We have,
So, slope of tangent
And slope of normal
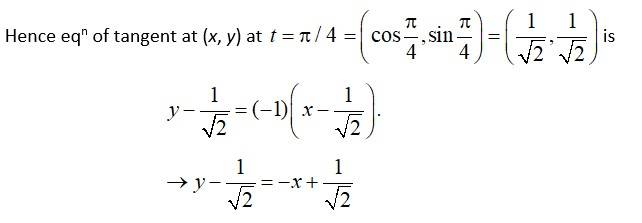
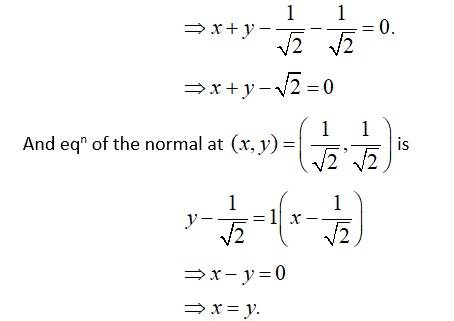
New answer posted
7 months agoContributor-Level 10
Diffrentiating wrt. X we get,
(i) When the tangent is to x-axis, the slope of tangent is 0
ie,
putting this in the eqn of curve. We get,
The point at which the tangents are parallel to x-axis are
(ii) When the tangent is parallel to y-axis, the slope of the normal is 0.
ie,
, putting this in the eqn of curve we get,
The point at which the tangents are parallel to y-axis are
New answer posted
7 months agoContributor-Level 10
The given eqn of the curve is
Slope of tangent to the curve is
Given,
When
The point of contact of the tangent to the curve is
The eqn of the line is
New answer posted
7 months agoContributor-Level 10
The given eqn of curve is
Slope of tangent to the curve is
Given,
which is not possible
we conclude that there is no possible tangent to the given curve with slope = 2.
New answer posted
7 months agoContributor-Level 10
The given eqn of curve is
Slope of tangent to the given curve is
Given that, slope of tangent = 1.
ie, X=1+1 or
or
When
and when
Hence, the point of contact of the tangents are
The reqd. eqn of line are
and
and
and
New answer posted
7 months agoContributor-Level 10
The given eqn of the curve is
slope of tangent to the curve
Then eqn of tangent is which gives us slope
So,
When x = 2,
And when x = 2,
The point when put into we get
which is true.
and the point when put into gives,
which is not true.
Hence, the required point is
New answer posted
7 months agoContributor-Level 10
Let the point joining the chord be
Then slope of the chord
= 2
The given eqn of the curve
slope of the tangent to the curve
Given that, the tangent is parallel to the chord PQ.
slope of tangent = slope of PQ.
and
The required point on curve is
New answer posted
7 months agoContributor-Level 10
The given eqn of the curve is
slope of tangent to the given curve,
when the tangent is parallel to x-axis
x = 3 or x = -1
When x = 3,
And when x = -1
Hence, the required points are
New answer posted
7 months agoContributor-Level 10
The given eqn of the curves are
so,
Slope of tangent to curve at is
Hence, slope of normal to curve
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
