Application of Derivatives
Get insights from 282 questions on Application of Derivatives, answered by students, alumni, and experts. You may also ask and answer any question you like about Application of Derivatives
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
We have,
At f(x) = 0.
x = 1 and x = -1.
At
At x = -1,
The maximum value of f(x)
Hence, option (D) is correct.
New answer posted
7 months agoContributor-Level 10
The equation of the given curve is
x2 = 2y.
Let p (x, y) be a point on the curve.
The distance of p (x, y) from (0, 5) is say S is given by
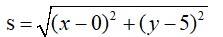
Let z = s2 = x2 + y2 + 25 – 10y = 2y + y2 -10y + 25
z = y2 – 8y + 25
So,
At
At y = 4,
y = 4, is point of minimum distance.
So, x2 = 2y->x2 = 2 * 4-> x2 = 8
Hence, the point of the nearest distance are and
Option (A) is correct.
New answer posted
7 months agoContributor-Level 10
Let r, h, l and Ø be the radius, height, slant height and semi-vertical angle respectively of the cone. i.e., r, h, l>0.
Then, Volume V of the cone is
So,

New answer posted
7 months agoContributor-Level 10
Let r and h be the radius and height of the cone.
The volume V of the cone is.
And curve surface area S is

New answer posted
7 months agoContributor-Level 10
Let r and h be the radius and height of the one in scribed in the sphere of radius R.
Then, is ΔOBC, rt angle at B (h-r)2 + r2 = R2
h2 + R2- 2hR + h2 = R2
r2 = 2hR -h2
Then the volume v of the cone is,
At
4Rh – 3h2 = 0.
h(4R – 3h) = 0.
h = 0 and
As h> 0,
At
is a point of maxima.
and
Hence, Volume of Cone,
Volume of sphere.
New answer posted
7 months agoContributor-Level 10
Let x and y in 'm' be the length of side of the square the radius of the circle respectily
Then, length of wire = perimeter of square + circumference of circle
28 = 4x + 2πy
2x + πy = 14
The combine area A of the square and the circle is
A = x2 + πy2
So,
At,
At,
isa point of minima
Hence, length of square =
and length of circle = 2πy
New answer posted
7 months agoContributor-Level 10
The volume v of a cylinder of height h and radius r is
V = πr2h = 100
Let, s be the surface area then
S = 2r2hr(r + h) =
At,
At,
isa point of minimum
And
New answer posted
7 months agoContributor-Level 10
Let r and h be the radius and height of the cylinder
So, r, h > 0
The total surface area s is given by
S = 2πr(h + r) = content .
= content = x (say)
Then, the volume v of the cylinder
So,
For maximum,
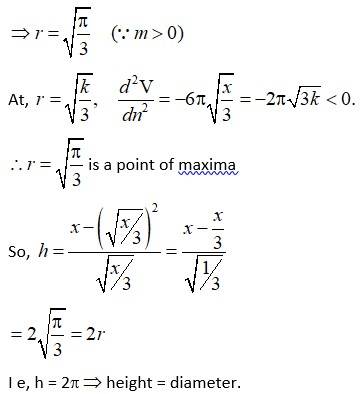
New answer posted
7 months agoContributor-Level 10
Let A.B.C.D.be the square increased in a given fixed circle with radius x
Let 'x' and 'y' be the length and breadth of the rectangle
∴x, y> 0
In ABC, right angle at B,
x2 + y2 = (2x)2
x2 + y2 = 4x2
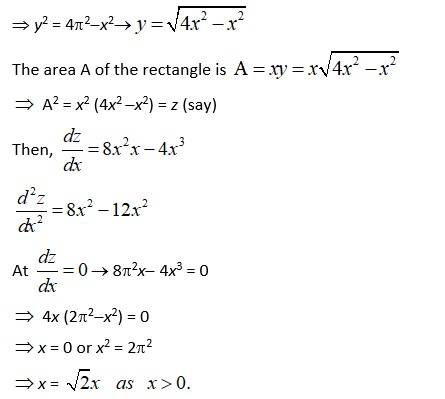
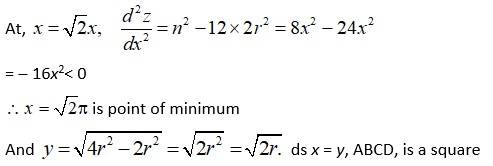
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers



