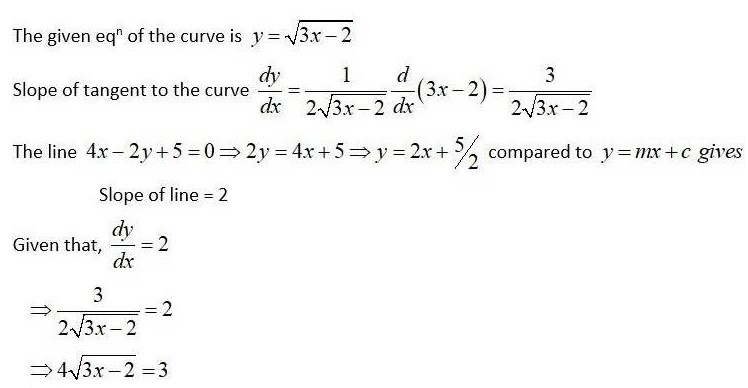Application of Derivatives
Get insights from 282 questions on Application of Derivatives, answered by students, alumni, and experts. You may also ask and answer any question you like about Application of Derivatives
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Let be the radius of the sphere &r be the error in measuring the radius.
Then, π = 9m and Δr = 0.03m.
Now, surface area S of the sphere is
S = 4πr2
So,
∴e, this = Δr = 8πr.Δr = 8π * 9 * 0.03
= 2.16πm3.
Appropriate error in calculating the surface area is 2.16πm3.
New answer posted
7 months agoContributor-Level 10
Let x be the radius of the sphere & Δπ be the error in measuring the radius.
Then, π = 7m and Δr = 0.02m.
Now, volume v of sphere is
So,
dv = 4π (7)2 (.0.02) = 3.92 πm3
∴The appropriate error is calculating the volume is 3.92πm3.
New answer posted
7 months agoContributor-Level 10
We know that, the surface area 5 of a 'x' when length cube, is S = 6x2.
So,
Given decrease in side,
New answer posted
7 months agoContributor-Level 10
We know that, the volume v of side 'a' mete of cube is v = x3.
So,
Given that, increase in side = 1% of x.
New answer posted
7 months agoContributor-Level 10
Given, y = f (x) = x3- 7x2 + 15.
So,
dy = (3x2- 14x) dx.
Δy = (3x2- 14x) Δx.
Let, x = 5 and Δx = 0.001. Then,
Δy = f (x + Δx) f (x).
f (x + Δx) = f (x) + Δy = f (x) + (3x2- 4x) Δx.
f (5 + 0.001) = 53- 7 (5)2 + 15 + [3 (5)2 - 14 (5)]. (0.001).
f (5.001) = 125 - 175 + 15 + (75 - 70) (0.001)
= -35 + 0.005 = - 34.995.
New answer posted
7 months agoContributor-Level 10
Given, y = f (x) = 4x2 + 5x + 2.
So, f (x) = 8x + 5. = 8x + 5 dy = (8x + 5) dx.
Let x = 2 and Δx = 0.01.Then,
f (x + Δx) = f (2 + 0.01) = f (2.01).
Δy = f. (x + Δx) f (Δx).
f (x +Δx) = f (x) +Δy.
= f (x) + dy = f (x) + (8x + 5) dx.
= f (2.01) = f (2) + (8 x 2 + 5). Δx {∴dx = Δx}
= 4 (2)2 + 5 (2) + 2 + 21 (0.01)
= 16 + 10 + 2 + 0.21 = 28.21.
New answer posted
7 months agoContributor-Level 10
(i) Let y= ?x : Let x = 25 and x = 0. 3.
Then, ?y = ?x+?x
= 5 + dy
=
= 5 + 0.03
(ii) ?49.5
A.(ii)
Let y = ?x Let x = 49 and x = 0.5.
Then,
= 7 + 0.0357.
(iii) ?0.6
A.(iii)
Let y = ?x Let x = 0.64 and ?x = 0.04.
Then,
= 0.8 - 0.025.
= 0.775.
(iv)
A.(iv)
Let Let x = 0.008 and ?x = 0.00 1.
Then, ?y =
= 0.2 + 0.0083.
= 0.208.
(v)
A.(v)
Let Let x = 1 and ?x = -0.001
Then,
= 0.999.
(vi)
A.(vi)
Let Then, x = 16 and ?x = 1.
Then,
(vii)
A.(vii)
Let Let x = 27 and ?x = 1.
Then,
(viii)
A.(viii)
Let Let x = 256 and ?x = 1.
Then,
(ix)
A.(ix)
New answer posted
7 months agoContributor-Level 10
The given eqn of curve is .
Then, differentiating wrt x we get,
which is the slope of the tangent to the curve.
The line compared to gives slope of line = 1.
Since, tangent is the line we have,
Putting y = 2 in we get,
Hence, the required point is
Option (A) is correct.
New answer posted
7 months agoContributor-Level 10
Given,
Slope of tangent,
So, slope of normal
Option (D) is correct.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers