Binomial Theorem
Get insights from 18 questions on Binomial Theorem, answered by students, alumni, and experts. You may also ask and answer any question you like about Binomial Theorem
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
5. Let (r + 1)th term be the general term of (x2–y)6.
So, Tr-1 = 6Cr (x2)6-r (-y)r
= (–1)r .6Cr . .
New answer posted
7 months agoContributor-Level 10
4. Let a5b7 occurs in (r + 1)th term of [removed]a – 2b)12.
Now, Tr+1 = 12Cra12-r (–2b)r
= (–1)r12Cra12–r . 2r. br
Comparing indices of a and b in Tr-1 with a5 and b7 we get, r = 7
So, co-efficient of a5b7 is (–1)712C7 27

New question posted
7 months agoNew question posted
7 months agoNew answer posted
7 months agoContributor-Level 10
2. 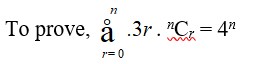
By binomial theorem,
(a + b)n = nC0 (a)n (b)0 + nC1 (a)n–1 (b)1 + …………. + nCr (a)n–r (b)r + …………… + nCn (a)n–n (b)n
Where, b0 = 1 = an–n
So, (a + b)n = nCr (a)n–r (b)r
Putting a = 1 and b = 3 such that a + b = 4, we can rewrite the above equation as
(1 + 3)n = nCr (1)n–r.3r
=>4n = .nCr
Hence proved.
New answer posted
7 months agoContributor-Level 10
1. For a number x to be divisible by y, we can write x as a factor of y i.e., x = ky where k is some natural number. Thus in order for 9n+1 – 8n – 9 to be divisible by 64 we need to show that 9n+1 – 8n – 9 = 64k where k is some natural number.
We have, by binomial theorem
(1 + a)m = mC0 + mC1 (a) + mC2 (a)2 + mC3 (a)3 + ………… + mCm (a)m
Putting, a = 8 and m = n + 1
(1 + 8)n+1 = n+1C0 + n+1C1.8 + n+1C2.82 + n+1C3.83 + ……. + n+1Cn+1. (8)n+1
=> 9n+1= 1 + (n + 1)8 + 82* [n+1C2 + n+1C3.8 + ………. + n+1Cn+1. (8)n+1–2] [since, n+1C0 = 1, n+1C1= n + 1]
=> 9n+1 = 1 + 8n + 8 + 64 * [n+1C2 + n+1C3.8 + ……�
New question posted
7 months agoNew question posted
7 months agoTaking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
