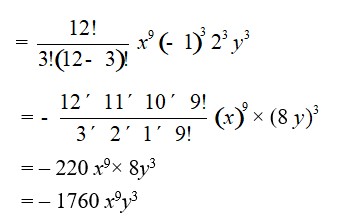Binomial Theorem
Get insights from 18 questions on Binomial Theorem, answered by students, alumni, and experts. You may also ask and answer any question you like about Binomial Theorem
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
15.
=
We know that by binomial theorem,
=
=
Then,
= (3x2)3 + + +
= 27x6 + + +
= 27x6 + + + [ ]
= 27x6 + [ ] + [ ] + [ ]
= 27x6 +
= 27x6– 54ax5 +
New answer posted
7 months agoContributor-Level 10
14. For (a – b) to be a factor of an – b nwe need to show (an – bn) = (a – b)k as k is a natural number.
We have, for positive n
an = =
=>an = nC0(a – b)n + nC1(a – b)n -1b + nC2(a – b)n – 2b2 + ………… +nCn-1 + nCnbn
=>an= + nC1 + nC2 + …………….…+ nCn-1 + [Since, nC0 = 1 and nCn = 1]
=> = +nC1 + nC2 + ……………… + nCn-1
=> = [ + nC1 + nC2 +……….…… + nCn-1 ]
=> = k where k = [ + nC1 + nC2 +……….…… + nCn-1 ] is a natural number.
Therefore (a – b) is a factor o
New answer posted
7 months agoContributor-Level 10
13. The general term of the expansion is
Tr+1 = 9Cr
= 9Cr
At r = 2,
T2+1 = 9C2
= 37a2x2
= / 37a2x2
= 36 *37a2x2
At r = 3,
T3+1 = 9C3
= 36a3x3
= 9'8'7'6!/3'2'1'6! 36a3x3
= 84 *36a3x3
Given that,
Co-efficient of = co-efficient of
=> 36 * = 84 *
=> = 36' 37 /84'36
=> =
=
New answer posted
7 months agoContributor-Level 10
1.The general term of the expansion (a + b)n is given by
Tr +1 = nCran–rbr
So, T1 = nC0an = an
T2 = nC1an-1b = an-1 b = an-1b = nan-1b
T3 = nC2an-2b2 = an-2b2 = an-2b2 = an-2b2
Given,
T1 = 729
=>an = 729 ------------------ (1)
T2 = 7290
=>nan–1b = 7290 ------------- (2)
T3 = 30375
=> an–2b2 = 30375 ------------------- (3)
Dividing equation (2) by (1) we get,
=
=> = 10
Similarly dividing equation (3) by (2) we get,
an–2b2 ÷ nan–1b =
=> an–2b2* =
=> * = * 2
=> =
=> =
=> 10 – = [since, &
New answer posted
7 months agoContributor-Level 10
11. The general term of the expansion is given by,
Tr+1 = mCr
= mCrxr
At r = 2,
T2+1 = mC2x2
Given that, co-efficient of x2 = 6
=>mC2 = 6
=> = 6
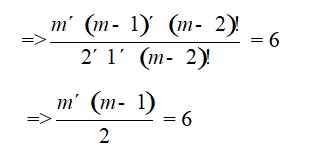
=>m2 – m = 12
=>m2 – m – 12 = 0
=>m2 + 3m – 4m – 12 = 0
=>m (m + 3) – 4 (m+ 3) = 0
=> (m – 4) (m + 3) = 0
=>m = 4 and m = –3
Since, we need a positive value of m we have, m = 4
New answer posted
7 months agoContributor-Level 10
10. General term of the expansion (1 + x)2n is
Tr+1 = 2nCr (1)2n-r(x)r
So, co-efficient of xn (i.e. r = n) is 2nCn
Similarly general term of the expansion (1 + x)2n–1 is
Tr+1 = 2n-1Cr (1)2n–1–rxr
And co-efficient of xn i.e. when r = n is 2n-1Cn
Therefore,
= 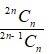
= ÷
= *
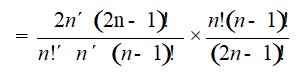
=
= 2
Thus, co-efficient of in = 2x co-efficient of in
New answer posted
7 months agoContributor-Level 10
9. The general term of the expansion (x +1)n is
Tr+1 = nCrxn–r1r
i.e. co-efficient of term = nCr
So, co-efficient of term =nC(r–1) – 1 = nCr – 2
Similarly, co-efficient of rth term = nCr – 1
Given that, nCr – 2 :nCr – 1 : nCr = 1 : 3 : 5
We have,
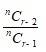
=
=> * =
=> =
=> =
=> 3r – 3 = n – r + 2
=> 3r + r = n + 2 + 3
=> 4r = n + 5 -------------- (1)
And,
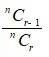
=
=> * =
=> =
=> =
=> 5r = 3n – 3r + 3
=> 5r + 3r = 3n + 3
=> 8r = 3n + 3 ----------------------- (2)
Multiplying equation (
New answer posted
7 months agoContributor-Level 10
8. The general term of the expansion (1 + a)m+n is
Tr+1 = m+nCrar [since, 1m+n-r = 1]
At r = m we have,
Tm+1 = m+nCmam
= (a)m
= am - (1)
Similarly at r = n we have,
Tn+1 = m+nCnan
= (a)n
= an - (2)
Hence from (1) & (2),
Co-efficient of am = Co-efficient of an =
New answer posted
7 months agoContributor-Level 10
6. Let (r + 1)th be the general term of (
So, Tr-1 = 12Cr (x2)12–r (–yx)r
= (–1)r12Crx24–2ryrxr
= (–1)r12Cr
= (-1)r12Cr
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers