Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
5 months agoContributor-Level 10
The Bond dissociation energy of D2 is greater than H2, therefore D2 reacts slower than H2.
New answer posted
5 months agoContributor-Level 10
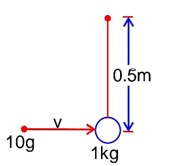
Velocity of bob after collision,
v1
From Conservation of Momentum,
->v = 400 m/s
New answer posted
5 months agoContributor-Level 10
Number of water molecule
Gypsum :- CaSO4.2H2O => 2
Plaster of paris :- CaSO4.
Dead burnt plaster : CaSO4 => 0
New answer posted
5 months agoContributor-Level 10
Velocity of bob after collision,
v1
From Conservation of Momentum,
->v = 400 m/s
New answer posted
5 months agoContributor-Level 10
Time taken by first drop to reach the ground,
Time for which second drop has fallen,
Height of the second drop
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers