Today, we will explore a fascinating concept, oscillation, towards the end of the Physics Class 11 textbook. Assuming you know, it’s a periodic back-and-forth motion of an object. But what exactly makes oscillation periodic? What possible characteristics can define an oscillatory motion of an object? Are there different types of oscillatory motions? Once we learn these motions, how will we calculate vector quantities, including velocity and acceleration?
This guide answers these questions in relation to Simple Harmonic Motion to help you better understand the oscillations chapter in the CBSE physics textbook for Class 11. All chapter sections are brief and simplified further here, so you can quickly refer to them as notes. This should help you revise quickly to score well and confidently during your annuals and engineering entrances.
- What is an Oscillation?
- Periodic Motion and Oscillatory Motion with Examples
- Simple Harmonic Motion Class 11
- Types of Repetitive Motion in Physics Class 11
- Relation Between SHM and Uniform Circular Motion
- Velocity and Acceleration in Simple Harmonic Motion
- Force Law for Simple Harmonic Motion
- Energy in Simple Harmonic Motion
- Simple Pendulum: An Example of SHM
- How to Study Oscillations Class 11
- A Note About the Reviewer
- NCERT Physics Class 11 Notes to Revise Quickly
- NCERT Solutions Physics Class 11 Chapters
What is an Oscillation?
An oscillation is a repeated back-and-forth or up-and-down motion of an object about a central or equilibrium position. This motion occurs after a displacement from the central position and a restoring force that pushes the object back to its original and stable position over and over again. This motion in its purest form is continuous and periodic, and one of its most common examples is a simple pendulum.
Periodic Motion and Oscillatory Motion with Examples
Periodic and oscillatory motions are two essential concepts in this 13th chapter of Physics class 11.
Periodic Motion
It is the type of motion of an object when it takes the same path within a defined and regular time interval.
Examples of Periodic Motion
- Earth rotates around the sun every year.
- A carousel horse moves up and down as the carousel rotates.
Periodic motion follows Newton's Second Law of Motion. You can explore all of Newton's Laws of Motion quickly!
So, now when an object moves up or down with a constant acceleration, like the carousel horse with mechanical force, the displacement has the equation derived from Newton's Second Law.
Oscillatory Motion
It’s a periodic motion where an object moves back and forth around an equilibrium position. Note that the equilibrium position is where the object rests without any external force.
You may even brush up now on two important concepts in early Class 11.
| Equilibrium of a Particle Class 11 Notes | Common Forces in Mechanics Class 11 |
Examples of Oscillatory Motions
- A spring that stretches and compresses when we pull and release it.
- An analogue metronome arm that swings side by side.
Oscillations vs Vibrations - They’re Not the Same
When talking about motion in physics, oscillations and vibrations differ in definition. Vibrations are faster than oscillations.
An example may help here. A playground swing moves up and down, or a suspension bridge moves in oscillatory motion, while a string instrument’s tuning fork, when struck, vibrates.
Period and Frequency
Having the above concepts clear, let’s get into two concepts.
- Period - It means it’s the amount of time an object requires to complete one full cycle motion. To recap, the period for Earth’s motion is one year.
- Frequency - It’s the cycles per second. We calculate frequency in Hertz. Formula is v = 1/T
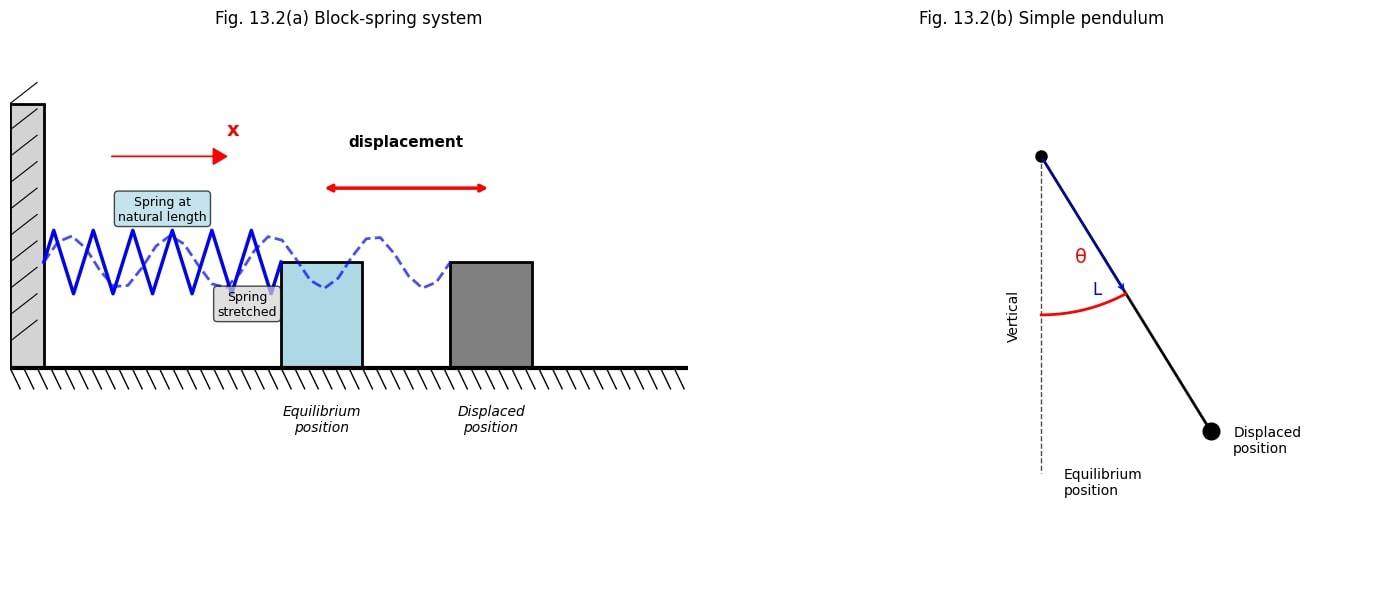
Displacement
Displacement in oscillations is learning how far the object has moved from equilibrium. Also, there are two different types of displacements. Linear and angular displacement.
The displacement is linear for a spring, as it moves up and down.
For a pendulum, the motion is right and left, and the displacement is angular.
Aligning with your NCERT textbook's figures 13.2 (a) and 13.2 (b) we have recreated the diagrams for oscillations and displacement below to help you visualise the concepts highlighted in this section.
Simple Harmonic Motion Class 11
Simple Harmonic Motion (SHM) is a pure form of oscillation. This is because it has a precise mathematical relationship between displacement and acceleration.
Let's simplify this SHM definition.
An object moves in a manner where displacement follows a sine or cosine wave. We use a sine wave to show the vertical height of the object at a point that's in motion around a circle over a specific period of time. The use of cosine wave is different here. It's the horizontal position of that same point over that same period of time.
Then comes the force. It's that which pulls the object back. It's the restoring force and is directly proportional to how far it’s from the centre.
The farther it is from the centre, the stronger the force becomes to pull it back. Now, think in a way that the further you stretch a rubber band, the stronger its pull is.
One essential thing to know when you are beginning to learn Simple Harmonic Motion is that this type of pure oscillation depends only on the position of the object, here, which is displacement. It does not depend on how fast the object is moving.
To describe Simple Harmonic Motion in physics, we use these terms, especially in Class 11.
Amplitude (A)
Amplitude or A is going to tell you the object’s distance when it swings away from its resting point. Just like how you’d pull a pendulum to one side, you can say that amplitude becomes the maximum distance from the middle point. We can also call it the maximum displacement from the mean or equilibrium position.
Period (T)
Using the same logic, the period tells us how much time it will take to complete one cycle for the object from its mean position to reach a specific amplitude and back to the same point. This is what we denote as a period.
Frequency (ν)
The next thing to know after amplitude and period is frequency. This related concept takes into account the number of cycles or periods occurring within one single second. It has an inverse relationship with period. In Class 11 Physics, we should remember that if the period is long, the frequency is small. The frequency can only be higher when the period is short.
Angular Frequency (ω)
To speed things up, we should know the speed or velocity of the object that moves within a cycle or period in terms of angles.
The angular frequency formula is: ω = 2π /T. Here, 2π radians means one full circle, and T is the period that we calculate as per second.
Phase (φ)
Phase is about where in the cycle the motion is right now. Think of it like looking at a clock.
The angle of the hand tells you exactly what time it is, right? Similarly, the phase tells you the position in the oscillation. You can easily find out if the object is at the top, bottom, or somewhere in between. It even gives you the direction: is it moving up or down from that point?
Another minor thing to distinguish here is the (φ) symbol is the Phase Constant. The SHM phase in general is denoted by (ωt + φ).
To understand all these terms used in SHM, we need to be clear about one more thing. So, in SHM, the object is moving constantly. It's not enough to know where the object is. Instead we should know when the object is where. So, if we know the specific moment in time (t), we can know the exact position (x) of the object at that particular instant. That's the displacement basically, and also what the SHM equation is all about.
Equation of SHM
The equation of SHM tells us about the object's position at a specific moment (or the displacement) using five coordinates.
- Amplitude
- Period
- Frequency
- Angular Frequency
- Phase
This basic equation of SHM is necessary to understand. Whether you are appearing for NEET Exams or other important competitive exams, score marks confidently that ask you any question on SHM.
Types of Repetitive Motion in Physics Class 11
For a quick glance before your exams.
| Feature |
Periodic Motion |
Oscillatory Motion |
Simple Harmonic Motion (SHM) |
| Definition |
It is any motion that repeats itself after a fixed time interval (period). |
This is a type of periodic motion. The object moves back and forth about a stable position. |
SHM is the purest form of oscillatory motion. The restoring force is directly proportional to the displacement from the mean/stable position. |
| Key Condition |
f(t) = f(t + T) |
Must be periodic and move about an equilibrium point. |
Restoring Force, F = -kx. The acceleration is also proportional to displacement (a ∝ -x). |
| Equation |
This is not defined by a single general equation. |
This is also not governed by a single general equation. |
x(t) = A cos(ωt + φ) |
| Examples |
Earth revolving around the Sun |
Swinging pendulum, mass on a spring, vibrating guitar string |
Mass on an ideal spring, simple pendulum (small oscillations) |
| All Are/Is? |
Not all periodic motion is oscillatory |
All oscillatory motion is periodic. |
SHM is a specific type of oscillatory motion. |
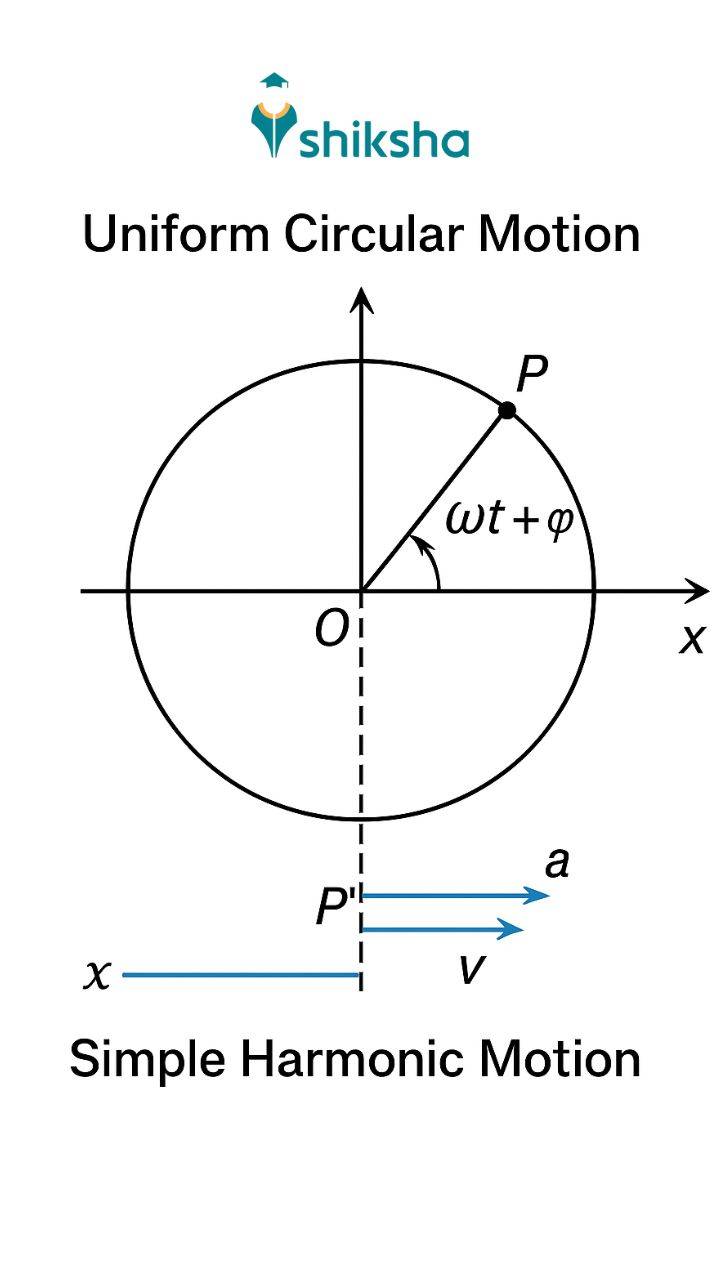
Relation Between SHM and Uniform Circular Motion
Your CBSE Physics textbook introduces the concept of uniform circular motion (where speed is constant but velocity changes with direction) to help you better understand simple harmonic motion from a geometrical (visual) perspective.
There could be a visual cue to learn SHM and UCM together.
Let’s say you are watching a particle moving in a circle from the side. It will be a straight line, isn’t it?
Now, we can project SHM equations of circular motions onto a straight line.
Velocity and Acceleration in Simple Harmonic Motion
Let’s see how exactly velocity, force, and acceleration work in Simple Harmonic Motion.
Velocity in Simple Harmonic Motion
We calculate the Velocity in SHM through this
When an object/particle moves in a circle, we show it as
Here,
ω is the angular frequency
A is the radius
For SHM, side-to-side, the velocity changes with time. And we represent that as
Note that the negative sign in this equation highlights that the direction is opposite to the displacement when it moves back to its centre.
Acceleration in SHM
When it is a uniform circular motion (UCM), there is a centripetal acceleration, and it remains constant. It will always point towards the centre of the circle.
When we project this acceleration onto the x-axis (our diameter of motion), we get the acceleration for SHM.
a(t) = -ω²Acos(ωt + φ)
And since we already know that the displacement is x(t) = Acos(ωt + φ), the equation simplifies into this.
a(t) = -ω²x(t)
Therefore,
This equation tells us two important things.
-
Magnitude: The acceleration is directly proportional to the displacement (a ∝ x). The farther the object is from the centre, the greater the magnitude of its acceleration.
-
Direction: The negative sign is the most important part to remember about SHM in Class 11. It means the acceleration is always directed opposite to the displacement. If the object is to the right (positive displacement), the acceleration is to the left (negative). Because it always pulls it back towards the centre. This is why the force is called a restoring force.
Force Law for Simple Harmonic Motion
Force plays a vital role in Simple Harmonic Motion. One of the givens here is that there should always be a restoring force to bring the oscillating object to its equilibrium. And in equilibrium there is no force.
Also, the magnitude of the restoring force is directly proportional to the displacement from the equilibrium position.
Now, this relationship can be understood better with Hooke’s Law. This pretty much applies to any solid material's elastic behaviour that can return to its original shape after being deformed up to a certain threshold.
F is the restoring force
K is the constant
X is the displacement
Energy in Simple Harmonic Motion
Simple Pendulum: An Example of SHM
How to Study Oscillations Class 11
A Note About the Reviewer
NCERT Physics Class 11 Notes to Revise Quickly
NCERT Solutions Physics Class 11 Chapters
Commonly asked questions
Why is uniform circular motion not SHM?
Uniform circular motion has constant speed. But SHM requires velocity and acceleration to vary sinusoidally with displacement. SHM is the projection of uniform circular motion. But it's not the motion itself, due to differing energy and force characteristics.
What is the force law for simple harmonic motion?
In SHM, the restoring force, F is directly proportional to the negative of displacement. That is, F=- kx. This follows Hooke’s law and ensures motion is oscillatory about the mean position with angular frequency,
At what displacement is the energy of a simple harmonic oscillation half kinetic and half potential?
For SHM, kinetic and potential energies are equal when displacement , where A is the amplitude. At this point, total energy is evenly shared between motion and position-dependent restoring forces.
Physics Oscillations Exam
Student Forum
Other Topics under this Chapter
Other Class 11th Physics Chapters
- Physics Mechanical Properties of Solids
- NCERT Class 11 Physics
- NCERT Class 11 Notes
- NCERT Notes
- Physics Motion in Plane
- Physics Mechanical Properties of Fluids
- Physics Motion in Straight Line
- Physics System of Particles and Rotational Motion
- Physics Oscillations
- Physics Waves
- Physics Thermal Properties of Matter
- Physics Motion
- Physics Gravitation
- Physics Thermodynamics
- Physics Work, Energy and Power
- Physics Units and Measurement
- Physics Laws of Motion