Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
49. We have,
sin 2x + cosx = 0.
2 sin cosx + cosx = 0 ( sin 2x = 2 sin xcosx)
cosx (2 sin x + 1) = 0.
cosx = 0 or 2 sinx + 1 = 0.
x = (2n + 1) , n∈z or sin x = = -sin = sin π + = sin
x = (2n + 1) , x∈z or x= nπ + (-1)n n∈z.
New answer posted
7 months agoContributor-Level 10
48. We have,
cos 3x + cosx-cos 2x = 0.
(cos 3x + cosx) cos 2x = 0
Using cos A + cos B = 2 cos cos
2 cos cos - cos 2x = 0.
2 cos cos - cos 2x = 0
2 cos 2xcosx - cos 2x = 0
cos 2x. (2 cosx - 1) = 0.
cos 2x = 0 or 2 cosx -1 = 0.
2x = (2n + 1) , n∈z or cosx = = cos
x = (2n + 1) , n∈z or x = 2nx± , n∈z.
New answer posted
7 months agoContributor-Level 10
47. We have,
cos 4x = cos 2x.
⇒ cos 4x-cos 2x = 0.
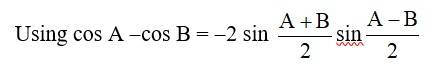
⇒ -2 sin sin = 0.
⇒sin sin = 0
⇒sin 3x sin x = 0.
∴sin 3x = 0 or sin x = 0
3x = nπ or x = nπ, n∈z,
⇒x = or x = nπ, n∈z
New answer posted
7 months agoContributor-Level 10
46. We have cosec x = 2 .i e, cosec x = (-)ve,
So, the principal solution lies in IIInd and IVth quadrent.
Now, cosec x = -2 = -cosec = cosec = cosec
So the principal solution are x = and
= and
= and
As cosec x = cosec ⇒sin x = sin
The general solution has the form,
x = nπ + (-1)n , n∈z.
New answer posted
7 months agoContributor-Level 10
45. We have, cot x = -√3 i.e., cot x is negative
So, the principal solution lies in IInd and IVth quadrant.
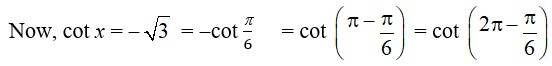
So the principal solution are a = and
= and
= and
As cot x = cot tan x = tan
The general solution has the form.
x = n+ , nz
New answer posted
7 months agoContributor-Level 10
43. tanx = √3
We have, tan x = √3
Since tan x is (+) ve the principal solution lies in Ist and IIInd quadrant
Now, tan x = √3 = tan . = tan
Principal solution are x = and
= and
= and .
As tan x = tan
The general solution is.
x = np + , n∈z
New answer posted
7 months agoContributor-Level 10
42. L.H.S. = cos 6x
= cos 3 (2x)
= 4 cos32x – 3 cos 2x [Q cos 3A = 4 cos3A – 3cos A]
= 4 [ (2 cos2x – 1)3] – 3 [ (2 cos2x – 1)] [Q cos 2x = 2 cos2x – 1]
= 4 [ (2 cos2x)3 + 3 [ (2 cos2x)2 (–1) + 3 (2 cos2x) (–1)2 + (–1)3] – 3 (2 cos2x) + 3
{Q (a + b)3= a3 + b3 + 3a2b + 3ab2}
= 4 [8 cos6x – 12 cos4x + 6cos2x – 1] – 6 cos2x + 3.
= 32 cos6x – 48 cos4x + 24 cos2x – 4 – 6cos2x + 3
= 32 cos6x – 48 cos4
New answer posted
7 months agoContributor-Level 10
41. L.H.S. = cos 4x.
= cos 2 (2x)
= 1 – 2 Sin2 (2x) [ cos 2x = 1 – 2 Sin2x]
= 1 – 2 [2 sin xcosx]2 [ sin 2x = 2 sin xcos x]
= 1 – 2 [4 sin2xcos2x]
= 1 – 8 sin2xcos2x
= R.H.S.
New answer posted
7 months agoContributor-Level 10
39. L.H.S. = cot x cot 2x – cot 2x cot 3x – cot 3x cot x.
= cot x cot 2x – cot 3x (cot 2x + cot x)
= cot x cot 2x – (cot 2x + cot x) [cot (2x + x)]
We know that,
we can write
= cot x cot 2x – cot 2x cot x + 1
= R.H.S.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
