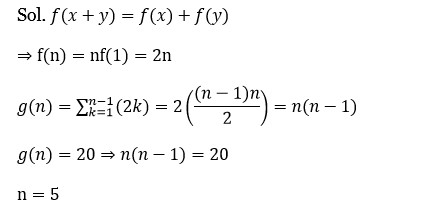Functions

For the Class of 2024 the Full time MBA graduates of the Rady School of Management of UC San Diego, the top functions for employment stood to be the following-

• Finance/Accounting- 27.8%
• Other-27.8%
• Consulting- 22.2%
• Marketing/Sales- 16.7%
• Operations/Logistics- 5.6%

$3-2^x-2^{1-x}\ge 0put{2}^x=t$

$3-t-\frac{2}{t}\ge 0\Rightarrow t^2-3t+2\le 0$

$\left(t-1\right)\left(t-2\right)\le 0\Rightarrow t\in \left[1,2\right]$

? P? = 6!/2! = 360

f (x) = 2e²? / (e²? +e? ) and f (1-x) = 2e²? / (e²? +e¹? )
∴ f (x) + f (1-x) = 1/2
i.e. f (x) + f (1-x) = 2
∴ f (1/100) + f (2/100) + . + f (99/100)
Σ? f (x/100) + f (1-x/100) + f (1/2)
= 49 x 2 + 1 = 99

lim? (x→7) (18- [1-x])/ ( [x-3a])
exist & a∈I.
= lim? (x→7) (17- [-x])/ ( [x]-3a)
exist
RHL = lim? (x→7? ) (17- [-x])/ ( [x]-3a) = 25/ (7-3a) [a ≠ 7/3]
LHL = lim? (x→7? ) (17- [-x])/ ( [x]-3a) = 24/ (6-3a) [a ≠ 2]
LHL = RHL
25/ (7-3a) = 8/ (2-a)
∴ a = -6

A function f (x) is continuous at x=1, so lim (x→1? ) f (x) = lim (x→1? ) f (x) = f (1).
Assuming a piecewise function like f (x) = { -x, x<1; ax+b, x1 } (structure inferred from derivative).
Continuity at x=1: f (1) = 1. a (1)+b = 1 => a+b=1.

The function is differentiable at x=1. The derivative of f (x) at x=1 from the left is -1. The derivative from the right is a.
So, a = -1. (The image has 2a = -1, which would imply a function like -x and ax²+b). Let's assume f' (x) = 2a for x>1.
2a = -1 => a = -1/2.

From a+b=1, b = 1 - a = 1 - (-1/2) = 3/2.
So, a = -1/2 and b = 3/2.

Given the function f (x) = cosec? ¹ (x) / √ {x - [x]} where [x] is the greatest integer function.

The domain of cosec? ¹ (x) is (-∞, -1] U [1, ∞).
For the denominator to be defined, x - [x] ≠ 0, which means {x} ≠ 0 (the fractional part of x is not zero). This implies that x cannot be an integer (x ∉ I).

Combining these conditions, the domain is all non-integer numbers except for those in the interval (-1, 1).

Kindly consider the following Image 

19.00
Only '2' in range → 1 function
one element out of 1, 3, 4 is in range with '2'
number of ways = ³C? * (3!/(2!1!)) * 2! = 18
(Select one from 1, 3, 4 and distribute among a, b, c)
Total function = 1 + 18 = 19

$y=lo{g}_{10}x+lo{g}_{10}{x}^{1/3}+lo{g}_{10}{x}^{1/9}+........upto\infty terms$

$=lo{g}_{10}x\left(1+\frac{1}{3}+\frac{1}{9}+......\right)$   

y = log₁₀ x * $\frac{1}{1-\frac{1}{3}}=\frac{3}{2}lo{g}_{10}x$  

Now, $\frac{2+4+6+....+2y}{3+6+9+....+3y}=\frac{4}{lo{g}_{10}x}$

$\Rightarrow \frac{2*y\frac{\left(y+1\right)}{2}}{3y\frac{\left(y+1\right)}{2}}=\frac{4}{lo{g}_{10}x}solo{g}_{10}x=6$

$\Rightarrow y=\frac{3}{2}*6=9$

So, (x, y) = (10⁶, 9)