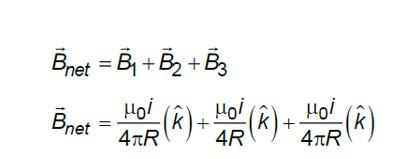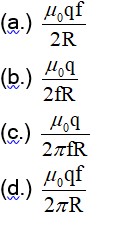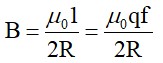Magnetic Field due to a Current Element

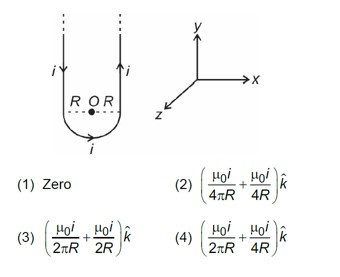
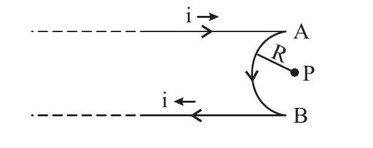
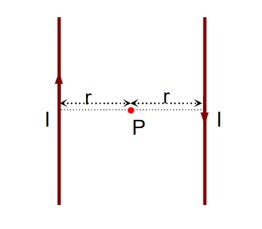
If currents are flowing in same direction, magnetic field will cancel each other, so the currents must flowing in opposite direction

$B_P=\frac{{\mu }_{0}I}{2\pi r}*2$

$\Rightarrow 300*10^{-6}=\frac{4\pi *10^{-7}}{2\pi *4*10^{-2}}*2$                                                                           

$\Rightarrow$ I = 30 A

When the ring rotates about its axis with a uniform frequency fHz, the current flowing in the ring is

I=q/T=qf

Magnetic field at the centre of the ring is

for $\pi R^{2}Area\to \text{'}l\text{'}$ current\

1 unit Area ® $\frac{l}{\pi R^2}$  

              $\pi r^2\to \frac{l}{\pi R^2}*\pi r^2$  

$i=\frac{l{r}^2}{R^2}$              

 

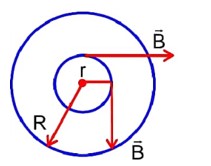
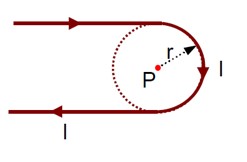
Now, consider Amperian loop of radius small 'r' ln Amperian loop magnetic field will be tangential to the amperian loop.

${\displaystyle ?\overrightarrow{B}.d\overrightarrow{i}={\mu }_0{l}_{enclosed}}$           (Ampere circuital law)

$B=\frac{{\mu }_0}{2\pi }\frac{l}{R^2}r$

$B\propto r$  

${\stackrel{?}{\mathrm{B}}}_{\mathrm{P}}={\stackrel{?}{\mathrm{B}}}_{\text{upper wire}}\otimes +{\stackrel{?}{\mathrm{B}}}_{\text{semi-circle}}?+{\stackrel{?}{\mathrm{B}}}_{\text{lower-wire}}\otimes$

$B_P=-\frac{{\mu }_{0}i}{4\pi R}+\frac{{\mu }_{0}i}{4R}-\frac{{\mu }_{0}i}{4\pi R}=\frac{{\mu }_0\mathrm{i}}{4\mathrm{R}}\left(1-\frac{2}{\pi }\right)$ pointing away from the page

In external magnetic field, a magnetic force acts on every small part of the loop in direction perpendicular to the wire. Thus, loop assumes a shape (circular) in which it covers maximum area

The magnetic field B is calculated as:
B = 2 * (μ? I / 4πr) + (μ? I / 4πr) = (μ? I / 4πr) * (2 + π)

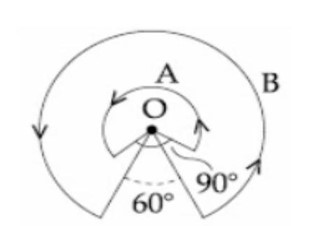
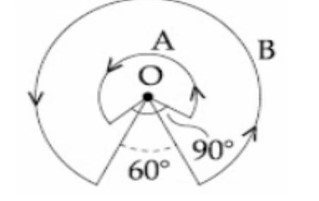
BA = μ?Iθ / 4πR
⇒ BA/BB = IAθARB / IBθBRA
⇒ (2(3π/2)(4)) / (3(π/3)(2))
⇒ 6/5

$B_A=\frac{{\mu }_{0}I\theta }{4\pi R}$

$\Rightarrow \mathrm{}\frac{B_A}{B_B}=\frac{I_A{\theta }_A{R}_B}{I_B{\theta }_B{R}_A}$

$\Rightarrow \frac{2\left(\frac{3\pi }{2}\right)\left(4\right)}{3\left. [\frac{5\pi }{3}\right]\left[2\right]}$

$\Rightarrow \mathrm{}\frac{6}{5}$

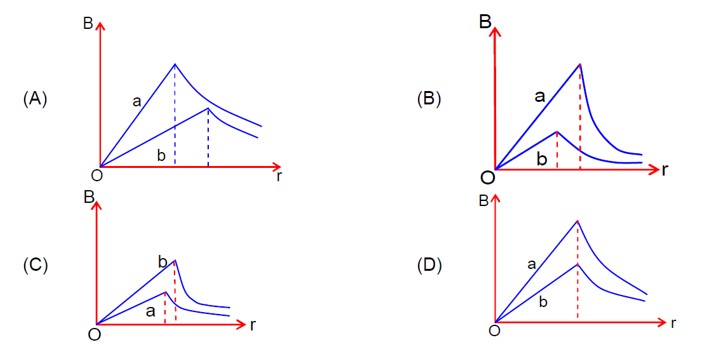
As b > a
The magnetic field inside the wire (rR) is B = µ? I/ (2πr).
For wire with radius a, B increases linearly to r=a, then decreases. For wire with radius b, B increases linearly to r=b, then decreases. Since a⇒ B? > B?
B? = µ? I / 2πa
B? = µ? I / 2πb
(Note: The question is likely asking for the graph representation, which is option A based on the formulas.)