How to Prepare and Remember a Trigonometric Table?

A Trigonometric table collectively represents the trigonometric values of standard angles for corresponding trigonometric ratios. The standard angles are 0°,30°,45°,60°,90°. The trigonometric ratios include Sine, Cosine, Tangent, Cotangent, Cosecant, Secant. Values for other angles like 180°,270°, 360°, etc., can also be calculated from the table by correlation between the values. For IIT JAM and JEE Main, knowing about this table is very important.

The trigonometry table:

Angle (in degrees)	0°	30°	45°	60°	90°	180°	270°	360°
Angle (in radians)	0°	π/6	π/4	π/3	π/2	π	3π/2	2πa
sin	0	1/2	1/√2	√3/2	1	0	-1	0
cos	1	√3/2	1/√2	1/2	0	-1	0	1
tan	0	1/√3	1	√3	∞	0	∞	0
cot	∞	√3	1	1/√3	0	∞	0	∞
cosec	∞	2	√2	2/√3	1	∞	.1	∞
sec	1	2/√3	√2	2	∞	‘-1	∞	1

Trigonometric value refers to a collective term for the values of different ratios, including tan, sec, cot, sine, cos and cosec in a trigonometric table.

 

 

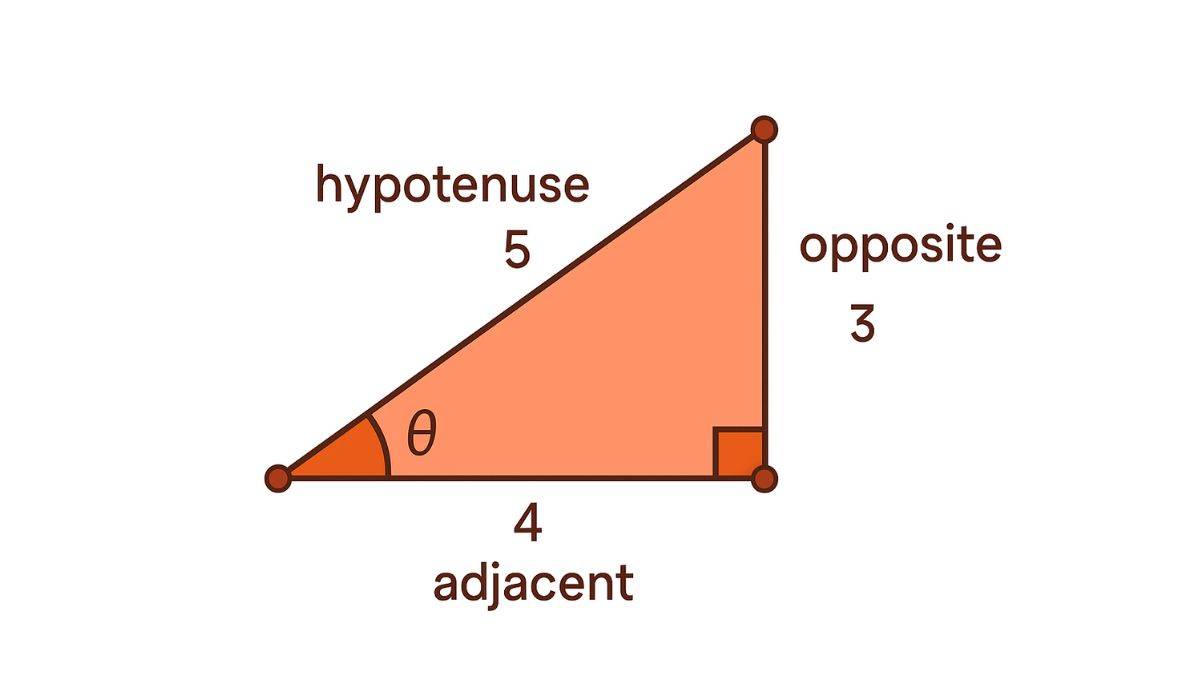
Let us consider the above right-angled triangle. It has a hypotenuse, an opposite side, and an adjacent side. The trigonometric values of different ratios will determined using the following ratios which are based on the calculation of the sides of triangle. NEET and CUET exam aspirants must be well aware of this. 

 

$$\sin \left(\theta \right)=\frac{\text{opposite}}{\text{hypotenuse}}=\frac{3}{5}$$ $$\cos \left(\theta \right)=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{4}{5}$$ $$\tan \left(\theta \right)=\frac{\text{opposite}}{\text{adjacent}}=\frac{3}{4}$$

$$\csc \left(\theta \right)=\frac{\text{hypotenuse}}{\text{opposite}}=\frac{5}{3}$$ $$\sec \left(\theta \right)=\frac{\text{hypotenuse}}{\text{adjacent}}=\frac{5}{4}$$ $$\cot \left(\theta \right)=\frac{\text{adjacent}}{\text{opposite}}=\frac{4}{3}$$

Let us discuss the steps to create a trigonometric table:

• Mention all the standard angles in a row, starting from 0 to 360. 
• All the trigonometric functions should be mentioned in the corresponding column. 
• Find the sine values for all the angles: Divide 0,1,2,3, and 4 by 4 sequentially and take the square root. For example, sin 0° = √0/4= 0, Sin 30° = √1/4= ½. This will give the values of standard angles between 0 and 90. To find out the values of 180° ,270°, 360°, use the formulae- sin(180° -x) = sinx

                                sin(180+x) = -sinx

                                sin(360° -x) = -sinx

• Find the Cos value: Cos values are the opposite of the values of sin angles in the table. Divide 4,3,2,1, and 0 by 4 sequentially and take the square root. You can also use the formula, cos = sin(90° -x)
• Find tan values: Calculate by the formula tanx = sinx/cosx. For example, if you have to calculate the value of tan30°, then first note that sin 30° = √3/2 and cos 30° = ½, so tan 30° = sin 30°/cos 30° = √3/2 by ½ = 1/√3.
• Find the cot, sec and cosec values by using the formulae cotx = 1/tanx,secx = 1/cosx, cosecx = 1/sinx respectively.

Things To Remember

You must remember the following trigonometric formula for creating a trigonometric table:

sinx = cos(90°-x) 

cosx = sin(90°-x) 

secx = cosec(90°-x) 

tanx = cot(90°-x) 

cotx = tan(90°-x) 

cosecx = sec(90°-x) 

1/sinx = cosecx

1/tanx = cotx 

1/cosx = secx

In order to remember the trigonometric table, you need to follow the below given steps:

1. First of all, you need to understand the layout of the trigonometric table.

θ	sin θ	cos θ	tan θ
0°	0	1	0
30°	1/2	√3/2	√3/3
45°	√2/2	√2/2	1
60°	√3/2	1/2	√3
90°	1	0	∞ (undefined)

2. Then, you need to use "√n / 2” Formula for Sine where n = 0,1,2,3,4

θ	n	sin θ = √n / 2
0°	0	0
30°	1	1/2
45°	2	√2/2
60°	3	√3/2
90°	4	1x

3. Now, you have got the table for sine θ, you need to write it in reverse for Cos θ

θ	cos θ
0°	1
30°	√3/2
45°	√2/2
60°	1/2
90°	0

4. Next rule is to remember that tan θ values are determined by dividing sin θ by cos θ

θ	tan θ
0°	0
30°	√3/3
45°	1
60°	√3
90°	∞ (undefined)

5. Use your left hand:

Thumb → 0°, Index → 30°, Middle → 45°, Ring → 60°, Little → 90°

To find sin θ:

Fold the relevant finger.

Count fingers below the fold → that's √n/2
(e.g. Fold middle finger = 2 below → sin 45° = √2/2)

For cos θ: Count fingers above the fold. 

• If tan(A+B) = √3 and tan(A-B) = 1/√3, then find the value of A and B, provided both A and B are acute angles. 

From the trigonometry table, we know tan 30° = 1/√3 and tan 60° = √3 

So, comparing those with the question, we can write, 

A+B = 60 ---- equation 1 

A-B = 30 ----equation 2 

Solving equations 1 and 2 we get, 

A= 45° and B = 15° . 

• If tan2A = cot(A-18°), where 2A is an acute angle, find the value of A.

We know that tanx = cot(90°-x) 

=> tan2A = cot(90°-2A)

=> cot(90°-2A) = cot(A-18°) { according to the question}

=> 90°-2A= A-18°

=> 3A= 108°

=> A= 36°

• Evaluate sin 60°cos 30° + sin 30°cos 60°

We know from the trigonometric table that sin 60°= ½, cos 30°= √3/2 sin 30° = √3/2, cos 60°= ½ 

So, putting the values in the question, we get 

½+√3/2 + √3/2+½ 

= 2+2√3/2