Maths

S = {n ∈ N | [n i; 0 1] [a b; c d] = [a b; c d] ∀a, b, c, d ∈ R}
[na+ic, nb+id; c, d] = [a, b;c, d]
This must be an identity matrix. n=1. The question seems to have typos. Let's follow the solution logic.
The solution implies the matrix must be [1 0; 0 1] or [-1 0; 0 -1]. And n must be a multiple of 8.
2-digit multiples of 8 are 16, 24, ., 96. Total 11 numbers.

Locus is auxiliary circle x²+y²=a²=4. (-1, √3) satisfies.

Ratio = ²? C? / (¹? C? + ¹? C? ) = ²? C? / ²? C? = 1.

M = {A = [a b; c d] | a, b, c, d ∈ {±3, ±2, ±1,0}
f (A) = det (A) = ad-bc=15
Case 1: ad=9 (2 ways: 3*3, -3*-3), bc=-6 (4 ways: 3*-2, -3*2, 2*-3, -2*3). Total = 2*4=8.
Case 2: ad=6 (4 ways), bc=-9 (2 ways). Total = 4*2=8.
Total no. of possible such cases = 8+8=16.

e? (dy/dx) - 2e? sinx + sinxcos²x = 0
d/dx (e? ) - (2sinx)e? = -sinxcos²x
I.F. = e^ (-∫2sinxdx) = e²cosx
Solution: e? e²cosx = -∫e²cosx sinx cos²x dx
Let cosx=t, -sinxdx=dt
∫e²? t²dt = e²? t²/2 - ∫2te²? /2 dt = e²? t²/2 - [te²? /2 - ∫e²? /2 dt] = e²? t²/2 - te²? /2 + e²? /4 + C
e^ (y+2cosx) = e²cosxcos²x/2 - e²cosxcosx/2 + e²cosx/4 + C
y (π/2)=0 ⇒ e? = 0 + 0 + e? /4 + C ⇒ C=3/4
y = ln (e²cosx (cos²x/2-cosx/2+1/4)+3/4e? ²cosx)
y (0) = ln (e² (1/2-1/2+1/4)+3/4e? ²) = ln (e²/4+3/4e? ²)
This seems very complex. The solution provided leads to α=1/4, β=3/4. 4 (α+β)=4.

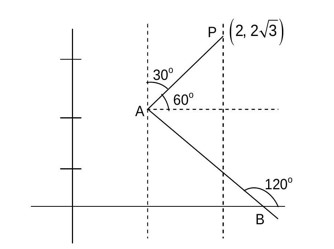
m (AP)=tan60°=√3. y-2√3=√3 (x-2). At x=1, y=√3. A= (1, √3).
m (AB)=tan120°=-√3. y-√3=-√3 (x-1) ⇒ √3x+y=2√3. (3, -√3) satisfies

(x+1)/ (x²/³-x¹/³+1) - (x-1)/ (x-x¹/²) = (x¹/³+1) - (1+x? ¹/²)
= (x¹/³ - x? ¹/²)¹?
general term = ¹? C? (x¹/³)¹? (-x? ¹/²)? = ¹? C? x^ (20-5r)/6)
For independent of x, 20-5r=0 ⇒ r=4
∴ Coefficient = ¹? C? = 210

Required probability = (? C? +? C? )/¹¹C? = 25/165=5/33.

p = 2i + 3j + k, q = I + 2j + k
r = αi + βj + γk is ⊥ to p+q and p-q
∴ r is collinear with (p+q) * (p-q) = -2 (p*q)
p*q = |i, j, k; 2,3,1; 1,2,1| = I - j + k
∴ r = λ (i - j + k)
|r| = √3 ⇒ λ = 1
∴ r = I - j + k = αi + βj + γk
⇒ α=1, β=-1, γ=1
|α|+|β|+|γ| = 3

| Class | No. of students | Number of possible cases |
| :-: | :-: | :- |
| 10 | 5 | (I) 2 | (II) 3 | (III) 2 |
| 11 | 6 | (I) 2 | (II) 2 | (III) 3 |
| 12 | 8 | (I) 6 | (II) 5 | (III) 5 |
Total cases =? C? *? C? *? C? +? C? *? C? *? C? +? C? *? C? *? C?
= 23,800 = 100K
∴ K = 238