Maths

  $\frac{dy}{dx}-\left(\frac{sin2x}{1+co{s}^{2}x}\right)y=\frac{sinx}{1+co{s}^{2}x}$

IF = $e^{-{\displaystyle \int \frac{sin2xdx}{1+co{s}^{2}x}}}$  

$=e^{ln\left(1+co{s}^{2}x\right)}=\left(1+co{s}^{2}x\right)$        

So, y(1 + cos² x) = ${\displaystyle \int \frac{sinx}{\left(1+co{s}^{2}x\right)}\cdot \left(1+co{s}^{2}x\right)dx}$  

y(1 + cos² x) = – cos x + c

$?$      y(0) = 0

0 = – 1 + c

-> c = 1

$y=\frac{1-cosx}{1+co{s}^{2}x}$   

Now, $y\left(\frac{\pi }{2}\right)=1$  

a, ar, ar², ….ar⁶³

a+ar+ar² +….+ar⁶³ = 7 [a + ar² + ar⁴ +.+ar⁶²]

$\frac{a\left(1-r^{64}\right)}{\left(1-r\right)}=7\frac{a\left(1-r^{64}\right)}{\left(1-r^2\right)}$            

1 + r = 7

r = 6

|2A| = 2⁷

8|A| = 2⁷

Now |A| = α²–β² = 2⁴

α² = 16 + β²

α²– β² = 16

(α–β) (α+β) = 16

->α + β = 8 and

α – β = 2

->α = 5 and β = 3

12x =

 $3x=\frac{\pi }{4}$

$cos3x=\frac{1}{\sqrt[]{2}}$

$4co{s}^{3}x-3cosx=\frac{1}{\sqrt[]{2}}$

$4\sqrt[]{2}co{s}^{3}x-3\sqrt[]{2}cosx-1=0$            

$x=\frac{\pi }{12}$ is the solution of above equation.

Statement 1 is true

$f\left(x\right)=4\sqrt[]{2}{x}^3-3\sqrt[]{2}x-1$

$f\text{'}\left(x\right)=12\sqrt[]{2}{x}^2-3\sqrt[]{2}=0$

$x=\pm \frac{1}{2}$

$f\left(-\frac{1}{2}\right)=-\frac{1}{\sqrt[]{2}}+\frac{3}{\sqrt[]{2}}-1=\sqrt[]{2}-1>0$            

f(0) = – 1 < 0

one root lies in $\left(-\frac{1}{2},0\right)$ , one root is $cos\frac{\pi }{12}$  which is positive. As the coefficients are real, therefore all the roots must be real.

Statement 2 is false.

$\underset{h\to 0}{lim}\frac{{\displaystyle {\int }_{\left(\frac{\pi }{2}-h\right)}^{{\left(\frac{\pi }{2}\right)}^3}cos\left(t^{1/3}\right)dt}}{h^2}$

$=\underset{h\to 0}{lim}\frac{0+3{\left(\frac{\pi }{2}-h\right)}^{2}cos\left(\frac{\pi }{2}-h\right)}{2h}$

$=\underset{h\to 0}{lim}\frac{3{\left(\frac{\pi }{2}-h\right)}^{2}sinh}{2h}$

$=\frac{3{\pi }^2}{8}$

P (2 obtained on even numbered toss) = k (let)

P (2) = $\frac{1}{6}$  

P (  $\overline{2}$ )= $\frac{5}{6}$  

$k=\frac{5}{6}*\frac{1}{6}+{\left(\frac{5}{6}\right)}^3*\frac{1}{6}+{\left(\frac{5}{6}\right)}^5*\frac{1}{6}+...$

$=\frac{\frac{5}{6}*\frac{1}{6}}{1-{\left(\frac{5}{6}\right)}^2}$

$=\frac{5}{11}$

n P (A) = 2⁷ = 128

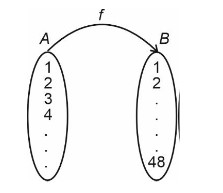
f : A → B

Number of function = 128 * 128….128 = 128⁷

$={\left(2^7\right)}^7=2^{49}$

->mⁿ = 2⁴⁹

m + n = 49 + 2 = 51

$N={\displaystyle \sum _{}^{}f}=27$

$\left(\frac{N}{2}\right)=\frac{27}{2}=13.5$

So, we have median lies in the class 12 – 16

I₁ = 12, f = 8, h = 4, c.f. = 13

So, here we apply formula

$M=I_1+\frac{\frac{N}{2}-c.f.}{f}*h=12+\frac{13.5-13}{8}*4$

$=12+\frac{5}{2}$

$M=\frac{24.5}{2}=12.25$

20 M = 20 * 12.25

= 245

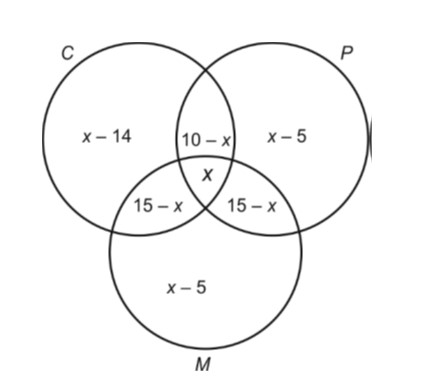
n (C) = 16, n (P) = 20, n (M) = 25

n (MÇP) = n (MÇC) = 15, n (PÇC) = 10,

n (MÇCÇP) = x.

n (CÈPÈM) £ n (U) = 40

n (CÈPÈM) = n (C) + n (P) + n (M) – n (C? M) – n (PÈM) – n (CÇP) + n (CÇPÇM)

40 ³ 16 + 20 + 25 – 15 – 15 – 10 + x

40 ³ 61 – 40 + x

19 ³ x

So maximum number of students that passed all the exams is 19.

$I=9{\displaystyle \underset{0}{\overset{9}{\int }}\left[\sqrt[]{\frac{10x}{x+1}}\right]dx}$

$=9\left[{\displaystyle \underset{0}{\overset{1/9}{\int }}0dx}+{\displaystyle \underset{1/9}{\overset{2/3}{\int }}dx}+{\displaystyle \underset{2/3}{\overset{9}{\int }}2dx}\right]$

$=9\left[\frac{2}{3}-\frac{1}{9}+2\left[9-\frac{2}{3}\right]\right]$

$=9\left[\frac{5}{9}+2*\frac{25}{3}\right]$

= 5 + 6 * 25

= 5 + 150

= 155