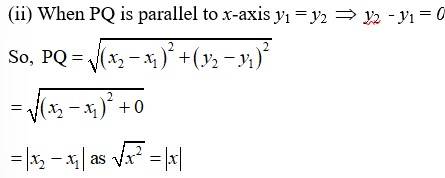Ncert Solutions Maths class 11th

11.

Let the two slopes be m and 2m. And if θ is the angle between the two lines.

$ta\mathrm{n\theta }=\left|\frac{m_1-m_2}{1+m_1{m}_2}\right|$

$\Rightarrow \frac{1}{3}=\left|\frac{2m-m}{1+2m..m}\right|=\left|\frac{m}{1+2m^2}\right|$

$\Rightarrow \frac{m}{1+2m^2}=\pm \frac{1}{3}($$\left|x\right|=\pm x)$

Case I. When $\frac{m}{1+2m}=\frac{1}{3}$

$\Rightarrow 3m=2m^2+1$

$\Rightarrow 2m^2-3m+1=0$

$\Rightarrow 2m^2-2m-m+1=0$

$\Rightarrow 2m\left(m-1\right)-\left(m-1\right)=0$

$\Rightarrow \left(m-1\right)\left(2m-1\right)-0$

$\Rightarrow m=1m=\frac{1}{2}$

Case II. When $\frac{m}{1+2m^2}=-\frac{1}{3}$

$\Rightarrow 3m=-\left(1+2m^2\right)$

$\Rightarrow 3m=-1-2m^2$

$\Rightarrow 2m^2+3m+1=0$

$\Rightarrow 2m^2+2m+m+1=0$

$\Rightarrow 2m\left(m+1\right)+\left(m+1\right)=0$

$\Rightarrow \left(m+1\right)\left(2m+1\right)=0$

$\Rightarrow m=-1m=-\frac{1}{2}$

Hence, $m=1,\frac{1}{2},-1m=-\frac{1}{2}$

$\therefore$ The possible slopes of the two lines (m, 2m) are (1, 2), $\left(\frac{1}{2},1\right),\left(-1,-2\right)$ and $\left(-\frac{1}{2},-1\right)$

10.

 Slope of line joining points A (3, –1) and B (4, –2) is

$m=\frac{-3-\left(-1\right)}{4-3}=\frac{-2+1}{1}=-1$

As slope of AB is the angle made by the line-segment AB w.r.t. x-axis, the angle between them is $$ and is given by $ta\mathrm{n\Theta }=m$

$\Rightarrow ta\mathrm{n\Theta }=-1\Rightarrow ta\mathrm{n\Theta }=-tan45°=tan\left(180°-45°\right)$

$\Rightarrow tan=tan135°$

$\Rightarrow =135°$

9.

Let A (–2, –1), B (4, 0), C (3, 3) and D (–3, 2) be the given points.

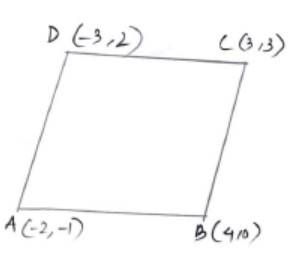
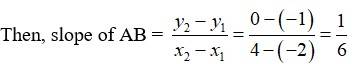
Slope of DC = $\frac{3-2}{3-\left(-3\right)}=\frac{1}{3+3}=\frac{1}{6}$

As slope of AB = slope of DC

We conclude that AB | | DC.

Similarly, slope of BC = $\frac{3-0}{3-4}=\frac{3}{-1}=-3$

Slope of AD = $\frac{2-\left(-1\right)}{-3-\left(-2\right)}=\frac{2+1}{-3+2}=\frac{3}{-1}=-3$

As slope of BC = slope of AD we conclude that BC | | AD.

Hence, as the pair of opposite sides of ABCD are parallel we can conclude that the given points are the vertices of a parallelogram.

8. Let P (x, –1), Q (2, 1) and R (4, 5) be the collinear points. Then,

Slope of PQ = Slope of QR

$\Rightarrow \frac{1-\left(-1\right)}{2-x}=\frac{5-1}{4-2}$

$\Rightarrow \frac{1+1}{2-x}=\frac{4}{2}$

$\Rightarrow 2*2=4\left(2-x\right)$

$\Rightarrow 4=8-4x$

$\Rightarrow x=\frac{4}{4}$

$\Rightarrow x=1$

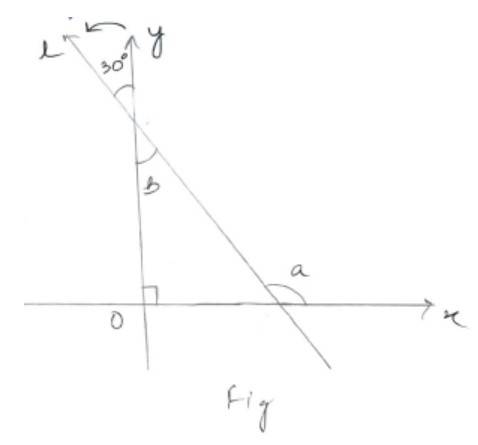
7. 

Let l be the line making 30° with y-axis as shown in figure. Then,

Angle a = $\angle b$ + 90° (Sum of exterior angle of a triangle)

$\Rightarrow \angle a=30°+90°$  ( $30°=\angle b$ vertically opposite angle)

$\Rightarrow \angle a=120°$

So, slope of line l = tan a

= m = tan 120°

= tan (180° – 60°)

= –tan 60°

$=-\surd 3$

6.

. Let the given point be A (4, 4), B (3, 5) and C (–1, –1)

Then, slope of AB, m₁ = $\frac{5-4}{3-4}=\frac{1}{-1}=-1$

Slope of AC, m₂ = $\frac{-1-4}{-1-4}=\frac{-5}{-5}=1$

And slope of BC, m₃ = $=\frac{-1-5}{-1-3}=\frac{-6}{-4}=\frac{3}{2}$

As m₁ – m₂ = –1 * 1 = –1

$\Rightarrow m_1=\frac{-1}{m_2}$

We conclude that AB and AC are perpendicular to each other.

Hence, ABC is a right-angle triangle right-angled at A

5.

Let 0 (0, 0) be the origin and A be the mid-point of line joining P (0, –4) and B (8, 0)

Then, co-ordinate of A = $\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)=\left(\frac{0+8}{2},\frac{-4+0}{2}\right)=\left(4,-2\right)$

$\therefore$ Slope of OA, m = $\frac{y_2-y_1}{x_2-x_1}=\frac{-2-0}{4-0}=-\frac{2}{4}=\frac{-1}{2}$

4.

Let A (x, 0) be the point on x-axis when is equidistant from P (7, 6) and Q (3, 4)

Then, PA = QA

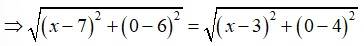
Squaring both sides, we get,

$\Rightarrow x^2-14x+49+36=x^2-6x+9+16$

$\Rightarrow 49+36-9-16=14x-6x$

$\Rightarrow 60=8x$

$\Rightarrow x=\frac{60}{8}=\frac{15}{2}$

$\therefore$ The required point on x-axis is $\left(\frac{15}{2},0\right).$

3.