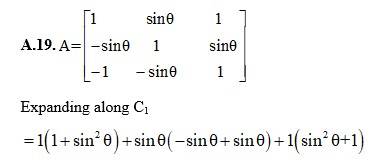Ncert Solutions Maths class 12th
Get insights from 2.5k questions on Ncert Solutions Maths class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Maths class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
Let 'x' cm be the length of edge of the cube which is a fxn of time t then,
= 3cm/s as it is increasing.
Now, volume v of the cube is v = x3
Ø Rate of change of volume of the cube
= 3x2.3
= 9x2
When x = 10cm.
= 9 x (10)2= 900
New answer posted
4 months agoContributor-Level 10
Let 'r' cm be the radius of the circle which is afxn of time.
Then, = 8 3cm/s as it is increasing.
Now, the area A of the circle is A = πr2.
So, the rate at which the area of the circle change πr2.
= 2πr 3
= 6πr.
When r = 10cm,
= 6.π * 10 = 60π
New answer posted
4 months agoContributor-Level 10
Let x be the length of edge,v be the value and s be the surface area of the cube then,
y = x3.
and S = 6x2, where x is a fxn of time.
Now,
(x3) = 8
(by chain rule)
3x2
Now, (bx2) = = 12x .
When x = 12 cm,
.
New answer posted
4 months agoContributor-Level 10
(a) r = 3cm
When r = 3 cm,
= 2 * π * 3 cm = 6π.
Thus, the area of the circle is changing at the rate of 6π cm .
(b) r = 4cm
whenr = 4cm,
= 2 * π * 4cm = 8π.
Thus, the area of the circle is changing at the rate of 8 .
New answer posted
4 months agoContributor-Level 10
Given equations are :-
This system of equation can be written, in matrix form, as AX= B, Where
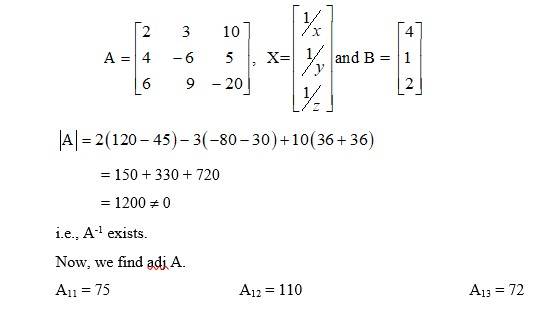
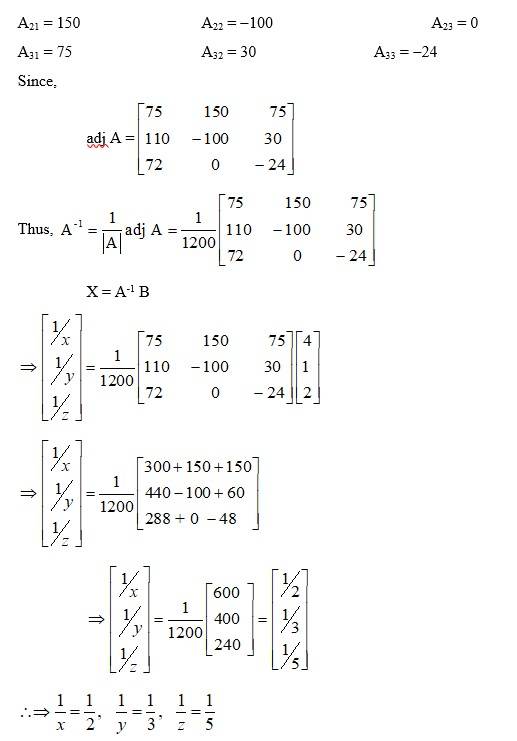
⇒ x = 2, y = 3, z = 5.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 687k Reviews
- 1800k Answers