physics ncert solutions class 11th
Get insights from 952 questions on physics ncert solutions class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about physics ncert solutions class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
5 months agoContributor-Level 10
(a) Let the mass of the sphere = m
Height of the plane = h
Velocity of the sphere at the bottom of the plane = v
At the top of the plane, the total energy of the sphere = potential energy = mgh
At the bottom of the plane, the sphere has both translational and rotational energies.
Hence, total energy = (1/2)mv2 + (1/2)I
Using the law of conservation of energy, we can write: (1/2)mv2+ (1/2)I = mgh …(1)
For a solid sphere, the moment of inertia, I = (2/5)mr2
The equation (1) becomes (1/2)mv2 + (1/2)( (2/5)mr2 = mgh
(1/2) v2 + (1/5)r2 = gh
From the relation v = , we get
(1/2) v2+ (1/5) v2= gh
v =
Since v depends on
New answer posted
5 months agoContributor-Level 10
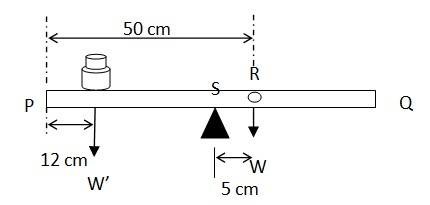
Mass of the meter stick = W
Mass of each coin = 5 g
When the coins are placed 12 cm away from the end P, the centre of mass gets shifted by 5 cm from point R towards the end P. The centre of mass is located at a distance of 45 cm from point P.
The net torque will be conserved for rotational equilibrium about point R,
10 x (45-12) – W' (50-45) = 0
W' = (10 x 33)/5 = 66 g
New answer posted
5 months agoContributor-Level 10
Radius of the original disc = R
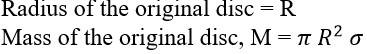

Mass of the smaller disc = = (1/4) = M/4
Let O and O' be the respective centers of the original disc and the cut out disc respectively. As per the definition of the centre of mass, the centre of mass of the original disc is supposed to be concentrated at O, while that of the smaller disc is supposed to be concentrated at O'.
It is given, OO' = R/2
After the smaller disc has been cut from the original, the remaining portion is considered to be a system of two masses. The two masses are
M – concentrated at O and M/4 concentrated at O'
Let x be the distance through which the centers of mas
New answer posted
5 months agoContributor-Level 10
Angular speed of the rotor, = 200 rad/s
Torque, = 180 Nm
Power required, P = x = 180 x 200 = 36 x103 W = 36 kW
New answer posted
5 months agoContributor-Level 10
Mass of the hollow cylinder, m = 3 kg
Radius of the hollow cylinder, r = 40 cm = 0.4 m
Applied force, F = 30 N
The MI of the hollow cylinder about its axis,
I = = 3 x 0.4 x 0.4 = 0.48 kgm2
Torque, = 30 x 0.4 = 12 Nm
For angular acceleration , torque is given by
= I x or
/ I = 12 / 0.48 = 25 rad/s
Linear acceleration = r x = 0.4 x 25 = 10 m/s2
New answer posted
5 months agoContributor-Level 10
(a) Initial angular velocity, = 40 rev/min, let the final angular velocity be
Let the moment of inertia of the boy with hands stretched be I1 and
M.I. with folded hands be I2
Given I2 = (2/5) I1
Since no external force acts on the boy, the angular momentum will remain constant.
Hence I1 = I2 , I1/I2) x = (5/2) x 40 = 100 rev/min
(b) Kinetic energy Ev = (1/2)I
Hence ( Final KE / Initial KE ) = (I2 )/ (I1 ) = { (2/5) I1 x 100 x 100 } / { I1 x 40 x 40 }
= 2.5
New answer posted
5 months agoContributor-Level 10
Mass of the cylinder, m = 20 kg
Angular speed, = 100 rad/s
Radius of the cylinder, r = 0.25 m
The moment of inertia of the solid cylinder
I = (1/2) mr2 = (1/2) x 20 x (0.25)2 = 0.625 m2
Kinetic energy = (1/2)I 2 = (1/2) x 0.625 x (100)2 = 3125 J
Angular momentum, L = I = 0.625 x 100 = 62.5 Js
New answer posted
5 months agoContributor-Level 10
Let m and r be the mass and radius of the hollow cylinder and solid sphere.
The moment of inertia of the hollow cylinder about its standard axis, =I
The MI of the solid sphere about an axis passing through its centre, Is = (2/5) mr2
We know the relation = I , where
= angular acceleration
= torque
I = moment of inertia
For the hollow cylinder, =
For the solid sphere, =
Since the torque applied is same, = , we get
= = (mr2) /( (2/5) mr2 )) = 5/2
Hence ……(i)
Now using the relation
+ where
= initial angul
New answer posted
5 months agoContributor-Level 10
(a)
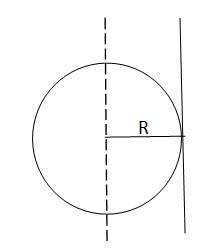
The moment of Inertia of a sphere about its diameter = 2MR 2/5
According to the theorem of parallel axis, the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and square of the distance between two parallel axes
Hence the moment of inertia about a tangent of the sphere = 2MR 2/5 + MR2 = 7MR 2/5
(b)
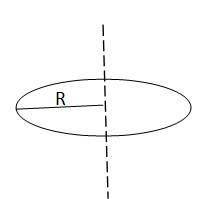
The moment of inertia of a disc about its diameter = MR 2/4
According to the theorem of perpendicular axis, the moment of inertia of a planar body about an axis perpendicular to its plane is equal to t
New answer posted
5 months agoContributor-Level 10

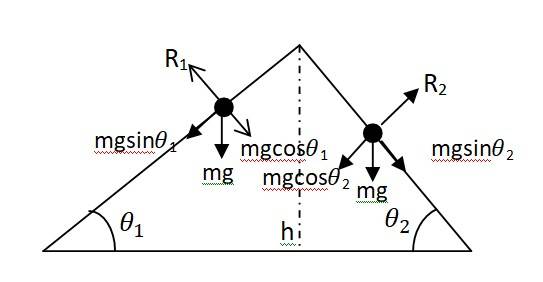
Mass of the car, m = 1800 kg
Distance between the front and rear axles, d = 1.8 m
Distance between C.G. and the front axle = 1.05 m
Let Rf and Rb be the force exerted from ground at front and rear axles respectively.
Rf + Rb = mg = 1800 x 9.8 N = 17640 N ……. (i)
For rotational equilibrium around C.G. we have Rf x 1.05 = Rb x (1.8 – 1.05)
Rf x 1.05 = Rb x 0.75
Rf/Rb = 0.75 / 1.05
Rf = 0.71 Rb ……. (ii)
From equation (i), we get
0.71 Rb + Rb = 17640
Rb = 10316 N
Rf = 7324 N
Therefore, force exerted on each front wheel = Rf/2 =7324/2 = 3662 N
Force exerted on each rear wheel, Rb/2 = 10316 / 2= 5158 N
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 686k Reviews
- 1800k Answers