Sequence and Series
Get insights from 114 questions on Sequence and Series, answered by students, alumni, and experts. You may also ask and answer any question you like about Sequence and Series
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
25. Let e and d the first term and common difference of an AP.
Then,
Sum of first p terms, Sp=a.
.
Similarly, Sq=b
----------------(2)
And. Sr=C
-----------------(3)
So, L.H.S. + (? given)
= + +
= + +
=c[q – r+r – p+p – q]+ [(p – 1)(q – r)+(q – 1)(r – p)+(r – 1)(p – q)]
=C * 0 + [pq – pr – q+r+qr – pq – r+p+pr=qr – p+q]
=0+ [pq – pq – pr+pr – q+q+r – r+qr+qr+p – p]
=
=0.
=R.H.S.
New answer posted
7 months agoContributor-Level 10
24. Let a and d be the first elements and common different of the A.P.
Then, Sum of first p terms of the AP=Sum of first q terms of A.P
Sp=Sq
p [2a+pd – d]=q [2a+qd – d]
2ap+p2d – pd=2aq+q2d – qd
2ap – 2aq+p2d – q2d – pd+qd=0
2a (p – q)+ [p2 – q2 – p+q]d=0.
2a (p – q)+ [ (p – q) (p+q) – (p – q)]d=0
(p – q) {2a+ [ (p+q) – 1]d}=0
Deviding both sides by p – q,
2a+ [ (p+q) –1]d=0.
And multiplying by P+Q/2 we get,
which in the form where n=p+q.
Sp+q=0.
New answer posted
7 months agoContributor-Level 10
23. Let a1, a2 be the first terms and d1, d2 be the common difference of the first term A.P.S
So,
---------------(1)
The ratio of their 18thterms.
=
=
= --------(2)
Comparing eqn (1) and (2),
=
So, ratio of their 18th terms =
New answer posted
7 months agoContributor-Level 10
22. Given, sum of n terms of A.P, Sn= (pn+qn2), p&q are constants substituting n=1,
S1=p* 1+q* 12=p+q=a1 [sum upto1st term only]
And substituting n=2,
S2=p* 2+q* 22=2p+4q=a1+q2 [sum upto 2ndtern only]
So, a1+a2=2p+4q
⇒ a2=2p+4q – a1=2p+4q – (p+q)=2p – p+4q – q
⇒ a2=p+3q
So, common difference, d=a2 – a1
= (p+3q) – (p+q)
=p+3q – p – q
=2q.
New answer posted
7 months agoContributor-Level 10
21. Given, ak =5k+1
Putting k =1,
a1 =5 * 1+1=5+1=6.
an =5n+1=l
So, sum of unto n teams of the AP, Sn =
Sn =
= .
New answer posted
7 months agoContributor-Level 10
20. The given A.P. is 25,22,19, …
So, a=25
d=22 – 25= –3
Given that, sum of first n terms of the AP=116.
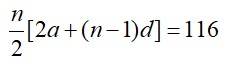
n [2 * 25+ (n – 1) (–3)]=116 * 2
n [50 – 3n+3]=232
n [53 – 3n]=232 .
53n – 3n2=232.
3n2 – 53n+232.
Using quadratic formula, a=3, b= –53, c=232.
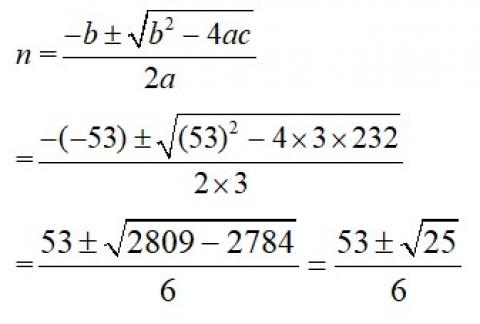
n = or
= or
= or 8.
As n N, n=8.
? Last term=a+ (n – 1)d
=a+ (8 – 1)d
=25+7* (–3)
=25 – 21
=4.
New answer posted
7 months agoContributor-Level 10
19. Let a and d be the first term and the common difference of an A.P.
Then, given ap =
a+(p – 1)d = --------(1)
and aq =
a+(q – 1)d = ---------(2)
Subtracting eqn (2) from (1) we get,
a+(p – 1)d – [a+(q – 1)d]=
a+(p – 1)d– a–(q– 1)d=
[(p – 1)–(q – 1)]d=
[p – 1 – q+1]d=
[p – q]d= .
d= .
Putting d= in eqn (1) we get,
.
.
So, sum of first pq terms,
= .
=
New answer posted
7 months agoContributor-Level 10
18. Let the sum of n farms of the A.P –6, , –5, …. gives –25.
Then,
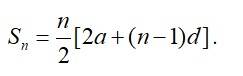
From the given A.P.
a= –6
d= –
So, –25=
–25 * 2=n
–50=n
–50=n
–50 * 2 =n[n – 25]=n2 – 25n
n2 – 25n+100=0.
n2 – 5n – 20n+100=0
n(n – 5) – 20(n – 5)=0
(n – 5)(n – 20)=0
So, n=5 and n=20.
When n=5
= –25.
When n=20
= = –120 + 19 * 5 = –120 + 95 = –25.
New answer posted
7 months agoContributor-Level 10
17. Given, a=2
Let A1, A2, A3, A4, A5, A6, A1, A6, A7, A10 be the first ten terms. So, A1=a.
Given A1+A2+A3+A4+A5= (A6+A1+A8+A1+A10)
a+ (a+d)+ (a+2d)+ (a+3d)+ (a+4d)
= [ (a+5d)+ (a+6d)+ (a+7d)+ (a+8d)+ (a+9d)]
5a+10d= [5a+35d].
4 [5a+10d]=9a+35d.
20a+40d=5a+35d.
40d – 35d=5a – 20a
5d= –15a
d= –3a
d= –3 * 2 [as a=2]
d= –6
So, A20=a+ (20 – 1)d
=2+19 * (–6)
=2 – 114
= –112.
New answer posted
7 months agoContributor-Level 10
16. Sum of all natural number between 100 and 1000 which are multiple of 5.
=105+110+115+ … +995.
So, a=105.
a=110 – 105=5.
As the last term is 995 which is the nthterm,
a+ (n – 1)d =995.
105+ (n – 1) * 5 =995.
(n – 1) * 5=995 – 105.
(n – 1)5 =890
n – 1 =
n =178+1
n =179
So, required sum Sn (a+l); l=last term.
= 179 * 550
=98450.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
