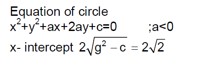Straight Lines
Get insights from 177 questions on Straight Lines, answered by students, alumni, and experts. You may also ask and answer any question you like about Straight Lines
- 177
Questions
- 0
Discussions
- 0
Active Users
- 0
Followers
Have a question about Straight Lines? Ask our experts
Keep it short & simple. Type complete word. Avoid abusive language.
The value of c for which line y = 2x + c is tangent to circle x2 + y2 = (√5)2 is
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
The value of c for which line y = 2x + c is tangent to circle x2 + y2 = (√5)2 is
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
By using condition of tangency,
c² = a² (m² + 1)
⇒ c² = 5 [ (2)² + 1]
⇒ c² = 25
⇒ c = ±5
Upvote 
Two sides of a parallelogram are along the lines 4x + 5y = 0 and 7x + 2y = 0. If the equation of one of the diagonals of the parallelogram is 11x + 7y = 9, then other diagonal passes through the point:
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Two sides of a parallelogram are along the lines 4x + 5y = 0 and 7x + 2y = 0. If the equation of one of the diagonals of the parallelogram is 11x + 7y = 9, then other diagonal passes through the point:
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
The point P(a,b) undergoes the following three transformations successively :
(a) reflection about the line y = x
(b) translation through 2 units along the positive direction of x-axis.
(c) rotation through angle π/4 about the origin in the anti-clockwise direction.
If the co-ordinates of the final position of the point P are (-1/√2, 7/√2), then the value of 2a + b is equal to :
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
The point P(a,b) undergoes the following three transformations successively :
(a) reflection about the line y = x
(b) translation through 2 units along the positive direction of x-axis.
(c) rotation through angle π/4 about the origin in the anti-clockwise direction.
If the co-ordinates of the final position of the point P are (-1/√2, 7/√2), then the value of 2a + b is equal to :
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
In an isosceles triangle ABC, the vertex A is (6, 1) and the equation of the base BC is 2x +y = 4. Let the point B lie on the line x + 3y = 7. If (α, β) is the centroid of ∆ABC, then 15(α + β) is equal to:
In an isosceles triangle ABC, the vertex A is (6, 1) and the equation of the base BC is 2x +y = 4. Let the point B lie on the line x + 3y = 7. If (α, β) is the centroid of ∆ABC, then 15(α + β) is equal to:
2x + y = 4
2x + 6y = 14
} y=2, x=3
B (1, 2)
Let C (k, 4–2k)
Now AB² = AC²
=> 5k² – 24k + 19 = 0
α = (6+1+10/5)/3 = 18/5
Now 15 (α+β)
15 (17/5) = 51
Upvote Let dy/dx = (ax-by+a) / (bx+cy+a), where a, b, c, are constants, represent a circle passing through the point (2, 5). Then the shortest distance of the point (11, 6) from this circle is:
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Let dy/dx = (ax-by+a) / (bx+cy+a), where a, b, c, are constants, represent a circle passing through the point (2, 5). Then the shortest distance of the point (11, 6) from this circle is:
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
dy/dx = (ax-by+a)/ (bx+cy+a)
=> bxdy + cydy + ady = axdx – bydx + adx
cy²/2 + ay – ax²/2 – ax + bxy = k
ax² + ay² + 2ax – 2ay = k
=> x² + y² + 2x – 2y = λ
Short distance of (11,6)
= √12²+5² – 5
= 13 – 5
= 8
Upvote Let a vector αi + βj be obtained by rotating the vector √3i + j by an angle 45° about the origin in counterclockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to :
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Let a vector αi + βj be obtained by rotating the vector √3i + j by an angle 45° about the origin in counterclockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to :
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Let z = αi + βj be a complex number & √3i + j = (√3 + i) where I = √-1.
|z| = |z - (√3 + i)| and |z| = |√3 + i| = 2.
This implies z lies on the perpendicular bisector of the segment from 0 to √3+i and on a circle of radius 2 centered at the origin.
z = (√3 + i) ( (1+i)/√2 )
z = (1/√2) [ (√3 - 1) + I (√3
Upvote Let A(-1,1), B(3, 4) and C(2,0) be given three points. A line y = mx, m > 0, intersects lines AC and BC at point P and Q respectively. Let A? and A? be the area of ?ABC and ?PQC respectively, such that A? = 3A?, then the value of m is equal to:
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Let A(-1,1), B(3, 4) and C(2,0) be given three points. A line y = mx, m > 0, intersects lines AC and BC at point P and Q respectively. Let A? and A? be the area of ?ABC and ?PQC respectively, such that A? = 3A?, then the value of m is equal to:
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Let the lengths of intercepts on x-axis and y-axis made by the circle x² + y² + ax + 2ay + c = 0, (a < 0) be 2√2 and 2√5, respectively. Then the shortest distance from origin to a tangent to this circle which is perpendicular to the line x + 2y = 0, is equal to :
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Let the lengths of intercepts on x-axis and y-axis made by the circle x² + y² + ax + 2ay + c = 0, (a < 0) be 2√2 and 2√5, respectively. Then the shortest distance from origin to a tangent to this circle which is perpendicular to the line x + 2y = 0, is equal to :
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Let L be a tangent line to parabola y² = 4x - 20 at (6,2). If L is also a tangent to the ellipse x²/2 + y²/b = 1, then the value of b is equal to:
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Let L be a tangent line to parabola y² = 4x - 20 at (6,2). If L is also a tangent to the ellipse x²/2 + y²/b = 1, then the value of b is equal to:
<!-- [if !supportLineBreakNewLine]-->
<!--[endif]-->
Parabola: y² = 4x - 20 = 4(x - 5). Vertex at (5,0).
Line: The text seems to derive the tangent equation y = x - 4. This is not a tangent to the given parabola. The standard tangent to y²=4aX is Y=mX+a/m. Here X=x-5, a=1. So y = m(x-5)+1/m.
The other curve is an ellipse: x²/a² + y²/b² = 1.
The text says
Upvote In a triangle PQR, the co-ordinates of the points P and Q are (-2, 4) and (4, -2) respectively. If the equation of the perpendicular bisector of PR is 2x - y + 2 = 0, then the centre of the circumcircle of the ΔPQR is:
In a triangle PQR, the co-ordinates of the points P and Q are (-2, 4) and (4, -2) respectively. If the equation of the perpendicular bisector of PR is 2x - y + 2 = 0, then the centre of the circumcircle of the ΔPQR is:
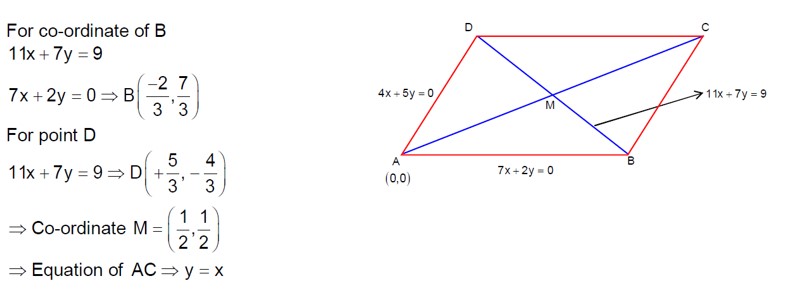
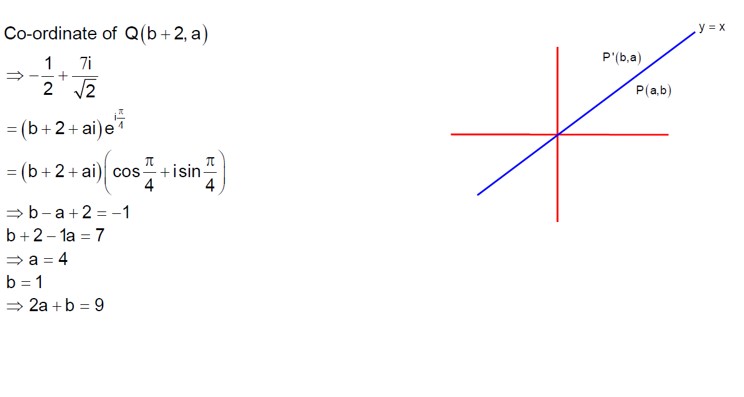
By property of triangle image of vertex of P is Q about the perpendicular side bisector of triangle Hence according to question X - Y = 0 is a perpendicular side bisector of PQ
Hence solving X - Y = 0 and 2X - y + 2= 0
o (-2, -2)
Upvote