Application of Derivatives

f(x) =   $\left|2x^2+3x?2\right|+sinxcosx$

$=\left|\left(2x?1\right)\left(x+2\right)\right|+sinxcosx$

$f\left(x\right)=\{\begin{array}{cc}\hfill ?2x^2?3x+2+sinxcosx,\hfill & \hfill 0<x<\frac{1}{2}\hfill \\ \hfill 2x^2+3x?2+sinxcosx,\hfill & \hfill \frac{1}{2}?x<1\hfill \end{array}$

$f\text{'}\left(x\right)=\{\begin{array}{cc}\hfill ?4x?3+cos2x,\hfill & \hfill 0<x<\frac{1}{2}\hfill \\ \hfill 4x+3+cos2x,\hfill & \hfill \frac{1}{2}?x<1\hfill \end{array}$            

 f(1) = 3 + sin 1 cos 1 and   $f\left(\frac{1}{2}\right)=sin\frac{1}{2}cos\frac{1}{2}$

$?f\left(1\right)+f\left(\frac{1}{2}\right)=3+\frac{sin2}{2}+\frac{sin1}{2}=3+\frac{1}{2}\left(sin1+sin2\right)$

$=3+\frac{sin1}{2}\left(1+2cos1\right)$

f(x) =   $\left|2x^2+3x-2\right|+sinxcosx$

$=\left|\left(2x-1\right)\left(x+2\right)\right|+sinxcosx$

$f\left(x\right)=\{\begin{array}{cc}\hfill -2x^2-3x+2+sinxcosx,\hfill & \hfill 0<x<\frac{1}{2}\hfill \\ \hfill 2x^2+3x-2+sinxcosx,\hfill & \hfill \frac{1}{2}\le x<1\hfill \end{array}$

$f\text{'}\left(x\right)=\{\begin{array}{cc}\hfill -4x-3+cos2x,\hfill & \hfill 0<x<\frac{1}{2}\hfill \\ \hfill 4x+3+cos2x,\hfill & \hfill \frac{1}{2}\le x<1\hfill \end{array}$            

 f(1) = 3 + sin 1 cos 1 and   $f\left(\frac{1}{2}\right)=sin\frac{1}{2}cos\frac{1}{2}$

$\therefore f\left(1\right)+f\left(\frac{1}{2}\right)=3+\frac{sin2}{2}+\frac{sin1}{2}=3+\frac{1}{2}\left(sin1+sin2\right)$

$=3+\frac{sin1}{2}\left(1+2cos1\right)$

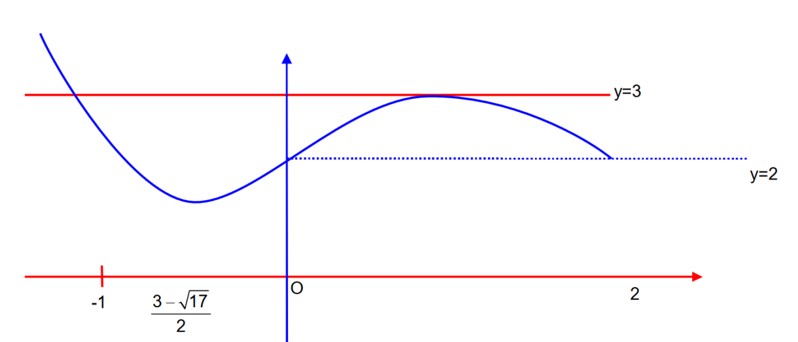
f (x) = 4log_e (x – 1) -2x² + 4x + 5, x > 1

    $(A)f\text{'}(x)=\frac{4}{x-1}-4x+4$

$\Rightarrow f\text{'}(x)>0\Rightarrow \frac{x\left(-x+2\right)}{x-1}>0$

option (A) is correct.

(B) f (x) = -1, has two solution

option (B) is correct

$\left(C\right)f"(x)=-\frac{4}{{\left(x-1\right)}^2}-4$                

$f\text{'}(e)-f"(2)=\frac{4e\left(2-e\right)}{e-1}+8>0$              

option (C) is not correct

(D) f (e) = 4log_e (e – 1) -2 (e² – 2e + 1) + 7 > 0

f (e + 1) = 4 – 2 (e + 1)² + 4 (e + 1) +5+ < 0

option (D) is correct   

Surface area, S = 4pr²

$?\frac{ds}{dt}=4?.2r\frac{dr}{dt}=8?\frac{dr}{dt}=constant=k\left(say\right)$                

$?\frac{ds}{dt}=k?s=kt+c$

$?4?r^2=kt+c$        

Initially t = 0, r = 3

c = 36 p

When t = 5, r = 7, k = 32p

When t = 9, r = r, r = 9

$?f_{\lambda }\left(x\right)=4\lambda x^3-36\lambda x^2+36x+48$

$f_{\lambda }\left(x\right)=12\left(\lambda x^2-6\lambda x+3\right)$

For increasing $f_{\lambda }\left(x\right)\ge 0$

$f_{\lambda }^{*}\left(x\right)=\frac{4}{3}{x}^3-12x^2+36x+48\therefore f_{\lambda }^{*}\left(1\right)+f_{\lambda }^{*}\left(-1\right)=73\frac{1}{2}-1\frac{1}{2}=72$

  $f\left(x\right)+f\left(x+k\right)=n\forall x\in R,\&k>0............\left(i\right)$

Replace x by x + k.          

$f\left(x+k\right)+f\left(x+2k\right)=n...............\left(ii\right)$

From (i) & (ii), f(x + 2k) = f(x).

$\therefore f\left(x\right)$  is periodic with period = 2k.

$I_1={\displaystyle \underset{0}{\overset{4nk}{\int }}f\left(x\right)}dx=2x{\displaystyle \underset{0}{\overset{2k}{\int }}f\left(x\right)dx}...................\left(ii\right)$

$I_2={\displaystyle \underset{-k}{\overset{3k}{\int }}f\left(x\right)}dx$ put x = t + k

$={\displaystyle \underset{-2k}{\overset{2k}{\int }}t\left(t+k\right)dt}=2{\displaystyle \underset{0}{\overset{2k}{\int }}f\left(t+k\right)dt}$

$=2n{\displaystyle \underset{0}{\overset{2k}{\int }}ndx}=4n^{2}k.$

Put x = cos 2θ

dx = -2 sin 2θ . dθ

$={\displaystyle \int \frac{1}{cos2\theta }tan\theta \left(-4sin\theta .cos\theta \right)d\theta }$

$g\left(\frac{1}{2}\right)=\mathcal{l}n\left|2-\sqrt[]{3}\right|+\frac{\pi }{3}$

= $\mathcal{l}n\left|\frac{\sqrt[]{3}-1}{\sqrt[]{3}+1}\right|+\frac{\pi }{3}$  

 $f\left(x\right)=\left|x^2-3x-2\right|-x$

$=\left|\left(x-\frac{3-\sqrt[]{17}}{2}\right)\left(x-\frac{3+\sqrt[]{17}}{2}\right)\right|-x$

$\Rightarrow f\left(x\right)=\left[\begin{array}{cc}\hfill x^2-4x-2-1\le x\le \frac{3-\sqrt[]{17}}{2}\hfill & \hfill -x^2+2x+2\frac{3-\sqrt[]{17}}{2}<x\le 2\hfill \end{array}\right]$

absolute minimum $f\left(\frac{3-\sqrt[]{17}}{2}\right)=\frac{-3+\sqrt[]{17}}{2}$

absolute maximum = 3

$\therefore sum3+\frac{-3+\sqrt[]{17}}{2}=\frac{3+\sqrt[]{17}}{2}$

Let z = x + iy

$\left|z-2\right|\le 1\Rightarrow \left|x-2+iy\right|\le 1$

(x – 2)² + y² $\le 1$

$z\left(1+i\right)+\overline{z}\left(1-i\right)\le 2$

$\left(x+iy\right)\left(1+i\right)+\left(x-iy\right)\left(1-i\right)\le 2$

$x+ix+iy-y+x-ix-iy-y\le 2$

x – y $\le 1$

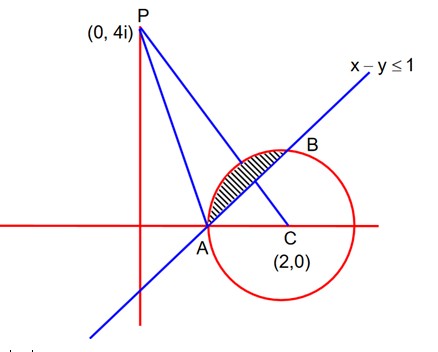
PD will be least as CP – r = DP, general pts on circle with centre (2, 0) is (2 + r cos, 0 + r sin )

here r = 1, (2 + cos , sin ) now slope of CP is $\frac{4-0}{0-2}=-2$

tan = 2

so D point will be $\left(2-\frac{1}{\sqrt[]{5}},\frac{2}{\sqrt[]{5}}\right)AP$ will be the greatest. A(1, 0)

now $\left|z_1^2\right|+\left|z_2^2\right|$

$={\left|1+0i\right|}^2+{\left|2-\frac{1}{\sqrt[]{5}}+\frac{2i}{\sqrt[]{5}}\right|}^2$

$=1+{\left(2-\frac{1}{\sqrt[]{5}}\right)}^2+\frac{4}{5}$

$=6-\frac{4}{\sqrt[]{5}}$

now $5\left({\left|z_1\right|}^2+{\left|z_2\right|}^2\right)=\alpha +\beta \sqrt[]{5}$

$5\left(6-\frac{4}{\sqrt[]{5}}\right)=\alpha +\beta \sqrt[]{5}$

= 30, = 4

+ = 26

Let perimeter of $\Delta$ is x and that of square is 22 – x

now area $=\frac{\sqrt[]{3}}{4}{\left(\frac{x}{3}\right)}^2+{\left(\frac{22-x}{4}\right)}^2$

for maximum or minimum,  $\frac{dA}{dx}=0$

x $=\frac{22\sqrt[]{3}}{\sqrt[]{3}+4}$

now side of a $\Delta =\frac{x}{3}$

$=\frac{22\sqrt[]{3}}{3\left(\sqrt[]{3}+4\right)}$

$=\frac{66}{}$$\frac{9}{}$$\frac{+}{}$$\frac{4}{}$