Class 11th

This is a Multiple Choice Questions type Questions as classified in NCERT Exemplar

Answer- b, d

Explanation – as we know f = $\mu N=\mu m_{1}gcos\theta$

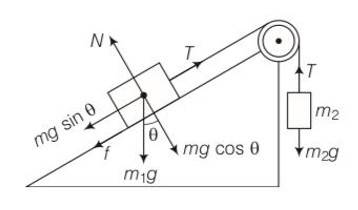
For system m₁+m₂ to move up

So m₂g- (m₁gsin $\theta +f$ )>0

So m₂g- (m₁gsin $\theta +\mu m_{1}gcos\theta$ )>0

So m₂>m₁ (sin $\theta +\mu cos\theta$ )

But if bodies moves downward

m₁gsin $\theta -f>m$ ₂g

m₁gsin> $\theta +\mu m_{1}gcos\theta$ m₂g

m₂1 (sinθ - uCosθ)

This is a Multiple Choice Questions type Questions as classified in NCERT Exemplar

Answer- a, b, d, e

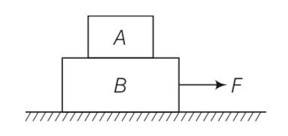
Explanation- suppose A and B are moving together a_common= $\frac{F-f_1}{m_A+m_B}=\frac{2\left(F-t_1\right)}{3m}$

Pseudo force = m_A (a_common)= $\frac{m}{2}*$ $\frac{2\left(F-t_1\right)}{3m}$ = $\frac{F-t_1}{3}$

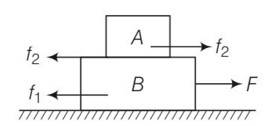
Force will be maximum when pseudo force and frictional force are equal to one another

$\frac{F_{max}-f_1}{3}$ = $?m_{A}g$

= 0.2 $*\frac{m}{2}*g=0.1mg$

F_max= 0.3mg+f₁

= 0.3mg+0.1 (3/2)mg= 0.45mg

(a) for F=0.25mgmax bodies will move together

(b) for F=0.5mg>F_max body A will slip with respect to B

(c) for F=0.5mg>F_max bodies will slip

This is a Multiple Choice Questions type Questions as classified in NCERT Exemplar

Answer- a, b, d

Explanation – x=0 for t<0s

X (t)=Asin4 $\pi t$  for 0

X=0, for t>1/4s

For,0 $\pi t$

Acceleration will be, a= dv/dt=-16 ${\pi }^2$ Asin4 $\pi t$

At t= 1/8 s, a (t)=-16 ${\pi }^2$ Asin4 $\pi \left(\frac{1}{8}\right)$ =-16 ${\pi }^2$ A

So force F =ma =-16 ${\pi }^2$ Am

Impulse = change in linear momentum = f (t)= -16 ${\pi }^2$ Am (1/4)

Impulse = change in linear momentum

=F $*t$ =-16 ${\pi }^{2}Am*\frac{1}{4}=-4{\pi }^{2}Am$

= -4 ${\pi }^2$ Am so clearly force depends upon a so force is also not constant .

The impulse (change in linear momentum)

At t=0 is same as t=1/4s

Clearly, force depends upon A which is not constant. Hence, force is also not constant.

This is a Multiple Choice Questions type Questions as classified in NCERT Exemplar

Answer- b

Explanation – mass of car m =0

Initial velocity =0,

velocity at east direction = v?

Time =2s

So v=u+at,

v? =0+a (2)

so a =v/2?

F=ma = $\frac{mv}{2}?$  so force = mv/2 towards east.

This is a Multiple Choice Questions type Questions as classified in NCERT Exemplar

Answer- b

Explanation-  we know that m= 5 kg

F= (–3? + 4? ) N and

initial velocity v= (6? -12? ) m/s

So retardation a= $\frac{F}{m}$  = ( $-\frac{3?}{5}+\frac{4?}{5}$ ) m/s²

We know v=u+at, for X-component only ,0 = 6? - $\frac{3?}{5}t$

So t= $\frac{5*6}{3}$ = 10s

This is a multiple choice answer as classified in NCERT Exemplar

Option (ii). Adding salt to water and

(iv). Decreasing the temperature of water

By adding salt to water,   the water molecule available at the surface to evaporate will be low and hence, the vapour pressure decreases. Also vapour pressure is directly proportional to temperature so when we decrease the temperature of water the vapour pressure decreases. 

This is a Multiple Choice Questions type Questions as classified in NCERT Exemplar

Answer- a

Explanation- x (t)= pt+qt²+rt³

V= dx/dt=p+2qt+3rt²

So a= o+2q+6rt

At t=2s a= 2q+6 $*$ 2 (r)

= 2q+12r

= 2 (4)+12 (5)=68m/s

So F =ma= 2 (68)= 136N

This is a multiple choice answer as classified in NCERT Exemplar

option (ii). High pressure and

(iii). Low temperature

The real gases obey the ideal gas equation, PV= nRT at low pressure and high temperature. So, a gas does not obey the ideal gas equation or behave ideally at high pressure and low temperature.

This is a Multiple Choice Questions type Questions as classified in NCERT Exemplar

Answer- c

Explanation –consider the adjacent diagram

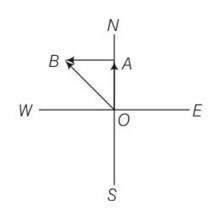
 OA= p₁= initial momentum of player northward

AB= p₂= final momentum of player towards west

OB= OA+AB

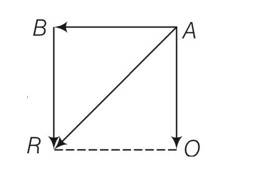
Change in momentum = P₂-P₁= AB-OA so we can say that AR will be along south west.

This is a Multiple Choice Questions type Questions as classified in NCERT Exemplar

Answer- d

Explanation-we know that for a system F_ext=dp/dt

If F_ext=0, dp =0,

P = constant

Hence, momentum of a system will remain conserve if external force on the system is zero.

In case of collision between particles, equal and opposite forces will act on individual particles by newton's third law.

according to newton's 2^nd law F=dp/dt

If F =0 then p = constant so momentum remains constant if external force is zero.