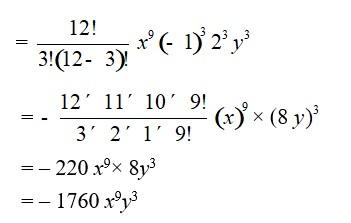Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
11. The general term of the expansion is given by,
Tr+1 = mCr
= mCrxr
At r = 2,
T2+1 = mC2x2
Given that, co-efficient of x2 = 6
=>mC2 = 6
=> = 6
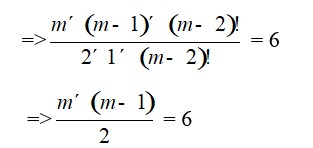
=>m2 – m = 12
=>m2 – m – 12 = 0
=>m2 + 3m – 4m – 12 = 0
=>m (m + 3) – 4 (m+ 3) = 0
=> (m – 4) (m + 3) = 0
=>m = 4 and m = –3
Since, we need a positive value of m we have, m = 4
New answer posted
7 months agoContributor-Level 10
10. General term of the expansion (1 + x)2n is
Tr+1 = 2nCr (1)2n-r(x)r
So, co-efficient of xn (i.e. r = n) is 2nCn
Similarly general term of the expansion (1 + x)2n–1 is
Tr+1 = 2n-1Cr (1)2n–1–rxr
And co-efficient of xn i.e. when r = n is 2n-1Cn
Therefore,
= 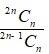
= ÷
= *
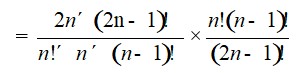
=
= 2
Thus, co-efficient of in = 2x co-efficient of in
New answer posted
7 months agoContributor-Level 10
9. The general term of the expansion (x +1)n is
Tr+1 = nCrxn–r1r
i.e. co-efficient of term = nCr
So, co-efficient of term =nC(r–1) – 1 = nCr – 2
Similarly, co-efficient of rth term = nCr – 1
Given that, nCr – 2 :nCr – 1 : nCr = 1 : 3 : 5
We have,
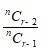
=
=> * =
=> =
=> =
=> 3r – 3 = n – r + 2
=> 3r + r = n + 2 + 3
=> 4r = n + 5 -------------- (1)
And,
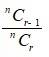
=
=> * =
=> =
=> =
=> 5r = 3n – 3r + 3
=> 5r + 3r = 3n + 3
=> 8r = 3n + 3 ----------------------- (2)
Multiplying equation (
New answer posted
7 months agoContributor-Level 10
8. The general term of the expansion (1 + a)m+n is
Tr+1 = m+nCrar [since, 1m+n-r = 1]
At r = m we have,
Tm+1 = m+nCmam
= (a)m
= am - (1)
Similarly at r = n we have,
Tn+1 = m+nCnan
= (a)n
= an - (2)
Hence from (1) & (2),
Co-efficient of am = Co-efficient of an =
New answer posted
7 months agoContributor-Level 10
6. Let (r + 1)th be the general term of (
So, Tr-1 = 12Cr (x2)12–r (–yx)r
= (–1)r12Crx24–2ryrxr
= (–1)r12Cr
= (-1)r12Cr
New answer posted
7 months agoContributor-Level 10
5. Let (r + 1)th term be the general term of (x2–y)6.
So, Tr-1 = 6Cr (x2)6-r (-y)r
= (–1)r .6Cr . .
New answer posted
7 months agoContributor-Level 10
4. Let a5b7 occurs in (r + 1)th term of [removed]a – 2b)12.
Now, Tr+1 = 12Cra12-r (–2b)r
= (–1)r12Cra12–r . 2r. br
Comparing indices of a and b in Tr-1 with a5 and b7 we get, r = 7
So, co-efficient of a5b7 is (–1)712C7 27
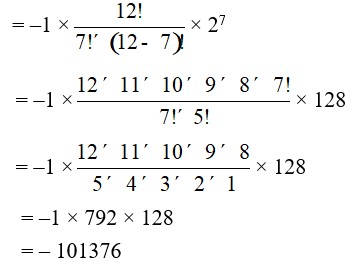
New question posted
7 months agoNew question posted
7 months agoTaking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers