Class 12th

1.20 ZnS shows Frenkel Defect.
AgBr shows Frenkel Defect and Schottky Defect. Frenkel Defect: It is a kind of defect in crystalline solids in which atoms are displaced from their lattice position 
to interstitial site creating vacancy at the lattice point. It usually occurs in ionic solid with large difference in size 
of ions.
Schottky Defect: This defect occurs when oppositely charged ions leave their lattice site creating vacancies in 
such a way that electrical neutrality of crystal is maintained. It is generally seen in highly ionic compounds where 
difference in size of cation and anion is small.

1.19 When a solid is heated, vacancy defect can arise. A solid crystal is said to have vacancy defect when some of the lattice sites are vacant. Vacancydefect leads to a decrease in the density of the solid.

1.18 Molar mass of the element = 2.7*10^-2 kg mol^-1
Edge length, a = 405 pm
Density, d = 2.7*10³ kg m^-3
Using the formula, d=? *? / ? ³NA
Putting the values given at their appropriate place, we get

(2.7 X 10³ )X (405 X 10^-12)3 X 6.022 X 10 / 2.7*10^-2 = 3.99 which is approximately equal to 4

Therefore, it is an fcc unit cell

1.17 Hexagonal close-packed lattice has the highest packing efficiency of 74%. The packing efficiencies of simple cubic and body-centered cubic lattices are 52.4% and 68% respectively

1.16 The atoms of element M occupy 1/3rd of the tetrahedral voids.

Therefore, the number of atoms of M is equal to 2 1/3 = 2/3rd of the number of atoms of N. Therefore, ratio of the number of atoms of M to that of N is M : N = (2/3):1 = 2:3 Thus, the formula of the compound is M₂N₃.

ccp= fcc = 6 * 1/2 + 8 X 1/8 = 4 = N atoms

Tetrahedral void= 8 (in fcc)

Number of M atoms = 8/3

So empirical formula = M 8/3 N₂ = M₂N₃

1.15 Number of atoms in close packaging = 0.5 mol

1 atom has 6.022*10²³ particles

So Number of particles in close-packed = 0.5 * 6.022 * 10²³ = 3.011*10²³

Number of tetrahedral voids = 2 * number of atoms in close packaging

Number of tetrahedral voids = 2 * 3.011 * 10²³= 6.022*10²³

Number of octahedral voids = number of atoms in close packaging

So the number of octahedral voids = 3.011 * 10²³

Total number of voids = Tetrahedral void + octahedral void

=6.022 * 10²³ + 3.011 * 10²³= 9.03*10²³

1.14  In square close-packed layer, a molecule is in contact with four of its neighbours. Therefore, the two-dimensional coordination number of a molecule in square close-packed layer is 4.

1.13   (i) An atom located at the corner of a cubic unit cell is shared by eight adjacent unit cells. Therefore, 1/8th portion of the atom is shared by one unit cell.
(ii) An atom located at the body centre of a cubic unit cell is not shared by its neighbouring unit cell. Therefore, the atom belongs only to the unit cell in which it is present i.e., its contribution to the unit cell is 1

1.12 

(ii) Face-centered unit cell: In a face-centered unit cell, the constituent particles are present at the corners 
and one at the centre of each face.
End-centered unit cell: An end-centered unit cell contains particles at the corners and one at the centre of 
any two opposite faces.

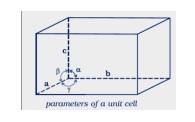
1.11 The six parameters that characterize a unit cell are as follows.
(i) Its dimensions along the three edges, a, b, and c these edges may or may not be equal.
(ii) Angles between the edges these are the angles (between edges b and c), (between edges a and c), and (between edges a and b)