Class 12th
Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 9
The expression for magnetic field depends on current carrying element , which is a vector quantity, therefore, statement-I is correct and statement-II is wrong.
New answer posted
3 months agoContributor-Level 10
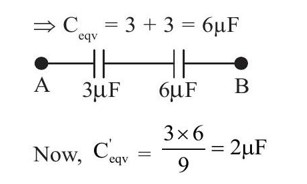
The circuit can be redrawn as an equivalent circuit given below
New answer posted
4 months agoContributor-Level 9
(P? ¹AP - I)²
= (P? ¹AP - I) (P? ¹AP - I)
= P? ¹A (PP? ¹)AP - P? ¹AP - P? ¹AP + I
= P? ¹A²P - 2P? ¹AP + I
= P? ¹ (A² - 2A + I)P = P? ¹ (A - I)²P
| (P? ¹AP - I)²| = |P? ¹ (A - I)²P| = |P? ¹| | (A - I)²| |P| = | (A - I)²| = |A - I|²
A - I = [1, 7, w²], [-1, w², 1], [0, -w, -w]
|A - I| = 1 (-w³ + w) - 7 (w) + w² (w) = -w³ + w - 7w + w³ = -6w.
|A - I|² = (-6w)² = 36w².
New answer posted
4 months agoContributor-Level 9
Let A = [a? ]? Sum of diagonal elements of A.A? is Tr (A.A? ) = ∑? ∑? a? ² = 9.
where each a? ∈ {0, 1, 2, 3}.
Case I: One of a? = 3 and rest are 0. (3²=9). There are? C? = 9 ways.
Case II: Two of a? are 2, one is 1, and rest are 0. (2² + 2² + 1² = 9). There are? C? *? C? = 36 * 7 = 252 ways.
Case III: One of a? = 2, five are 1, and rest are 0. (2² + 1²+1²+1²+1²+1² = 9). There are? C? *? C? = 9 * 56 = 504 ways.
Case IV: All nine a? = 1. (1² * 9 = 9). There is 1 way.
Total = 9 + 252 + 504 + 1 = 766.
New answer posted
4 months agoContributor-Level 9
A = lim (n→∞) (2/n) ∑ (r=1 to n) f (r/n + n/ (n²)
(The term n/n² seems intended to be part of the function argument, not simply added. The solution proceeds as if it's f (r/n)
A = lim (n→∞) (2/n) ∑ (r=1 to n) [ f (r/n) + f (1/n) + . + f (n-1)/n) ]
The expression in the image seems to be: A = lim (n→∞) (2/n) [ f (1/n) + f (2/n) + . + f (n-1)/n) ]
A = 2 ∫? ¹ f (x) dx = 2 ∫? ¹ log? (1 + tan (πx/4) dx
put πx/4 = t ⇒ dx = 4/π dt
A = 2 ∫? ^ (π/4) log? (1 + tan (t) * (4/π) dt = (8/π) ∫? ^ (π/4) log? (1 + tan (t) dt
Using the property ∫? f (x)dx = ∫? f (a-x)dx, the integral ∫? ^ (π/4) log (1 + tan (t)dt ev
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers